
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,
表示的数为-10,![]() ,点
,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)请你写出数轴上点![]() 对应的数;
对应的数;
(2)当运动的时间为3秒时,请你求出此时点![]() 、
、![]() 在数轴上对应的数,并求出
在数轴上对应的数,并求出![]() 、
、![]() 之间的距离;
之间的距离;
(3)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
【答案】(1)30;(2)点M、N在数轴上对应的数分别为-1和6,M、N之间的距离是7;(3)2秒或10秒
【解析】
(1)根据点A表示的数为-10,OB=3OA,可得点B对应的数;
(2)求出运动距离,即可求出点M、N在数轴上对应的数,M、N之间的距离;
(3)分①点M、点N在点O两侧;②点M、点N重合两种情况讨论求解.
解:(1)∵OB=3OA=30,
∴B对应的数是30.
故答案为:30.
(2)M:-10+3×3=-1,
N:2×3=6,
MN=7,
∴点M、N在数轴上对应的数分别为-1和6,M、N之间的距离是7;
(3)设经过x秒,点M、点N分别到原点O的距离相等,
此时点M对应的数为3x-10,点N对应的数为2x.
①点M、点N在点O两侧,
则10-3x=2x,
解得x=2;
②点M、点N重合,
则3x-10=2x,
解得x=10.
综上:经过2秒或10秒,点M、点N分别到原点O的距离相等.


科目:初中数学 来源: 题型:
【题目】按下列程序计算,把答案填写在表格里,然后看看有什么规律,想想为什么会有
这个规律?
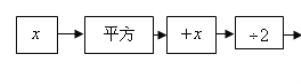
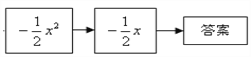
(1)填写表内空格:
输入 | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是____________.
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A在第一象限,AB⊥x轴于B.AC⊥y轴于C,A(4a,3a),且四边形ABOC的面积为48.
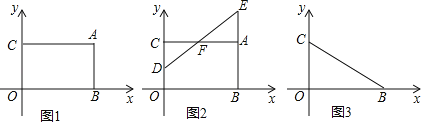
(1)如图1,直接写出点A的坐标;
(2)如图2,点D从O出发以每秒1个单位的速度沿y轴正半轴运动,同时点E从A出发,以每秒2个单位的速度沿射线BA运动,DE交线段AC于F,设运动的时间为t,当S△AEF<S△CDF时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连BN交y轴轴于P,当OM=3OP时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
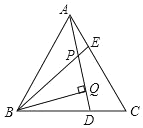
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△DCE均为等边三角形,点A. D.E在同一直线上,连接BE.
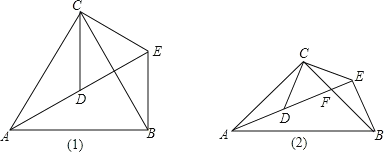
填空:(1),①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 ;
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,且交BC于点F,连接BE.若∠CAF=∠BAF,BE=2,试求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
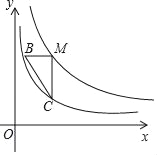
【题目】如图,点M在函数y=![]() (x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=
(x>0)的图象上,过点M分别作x轴和y轴的平行线交函数y=![]() (x>0)的图象于点B、C.
(x>0)的图象于点B、C.
(1)若点M的坐标为(1,3).
①求B、C两点的坐标;
②求直线BC的解析式;
(2)求△BMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
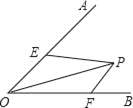
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=4,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于4,则α=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…嘉琪依次在小球上标上数字1,2,3,4,5,6,…,则从左往右第100个黄球上所标的数字为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com