
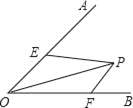
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=4,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于4,则α=_____.
【答案】30°
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=4,求出α的度数即可.
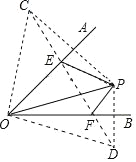
解:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=4,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=4,
∴OC=OD=CD=4,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故答案为:30°


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
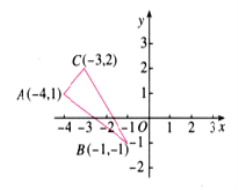
【题目】如图,利用关于坐标轴对称的点的坐标特点
(1) 作出△ABC关于x轴对称的图象.
(2) 写出A、B、C的对应点A′、B′、C′的坐标.
(3) 直接写出△ABC的面积__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,
表示的数为-10,![]() ,点
,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)请你写出数轴上点![]() 对应的数;
对应的数;
(2)当运动的时间为3秒时,请你求出此时点![]() 、
、![]() 在数轴上对应的数,并求出
在数轴上对应的数,并求出![]() 、
、![]() 之间的距离;
之间的距离;
(3)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:(1)AD上任意一点到点C、D的距离相等;(2)AD上任意一点到AB、AC的距离相等;(3)AD⊥BC且BD=CD;(4)∠BDE=∠CDF,其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
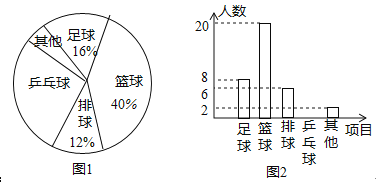
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
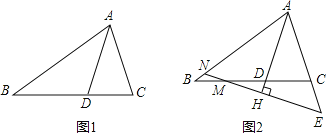
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC
(1)填空:如图1,∠B= °,∠C= °;
(2)如图2,若M为线段BC上的点,过M作MH⊥AD,交AD的延长线于点H,分别交直线AB、AC与点N、E.
①求证:△ANE是等腰三角形;
②线段BN、CE、CD之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
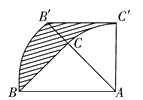
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决后面的问题
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘aa…,a记为an,如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
(1)计算下列各对数的值:log24=______,log216=______,log264=______;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是______;
(3)拓展延伸:下面这个一股性的结论成立吗?我们来证明logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴aman=am+n=MN,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
(4)仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga![]() (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)
(5)计算:log34+log39-log312的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离![]() .
.
利用数形结合思想回答下列问题:
(1)数轴上表示-2和1的两点之间的距离是______.
(2)数轴上表示![]() 和-1的两点之间的距离表示为______.
和-1的两点之间的距离表示为______.
(3)在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,且满足
,且满足![]() ,若
,若![]() 是数轴上任意一点,点
是数轴上任意一点,点![]() 表示的数是
表示的数是![]() ,当
,当![]() 时,
时,![]() 的值为多少?
的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com