
【题目】阅读下列材料并解决后面的问题
材料:对数的创始人是苏格兰数学家纳皮尔(J.Npler,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evler,1707--1783)才发现指数与对数之间的联系,我们知道,n个相同的因数a相乘aa…,a记为an,如23=8,此时,3叫做以2为底8的对数,记为log28,即log28=3一般地若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab,即logab=n.如34=81,则4叫做以3为底81的对数,记为log381,即log381=4.
(1)计算下列各对数的值:log24=______,log216=______,log264=______;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是______;
(3)拓展延伸:下面这个一股性的结论成立吗?我们来证明logaM+logaN=logaMN(a>0且a≠1,M>0,N>0)
证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴aman=am+n=MN,
∴logaMN=m+n,
又∵logaM=m,logaN=n,
∴logaM+logaN=logaMN(a>0且a≠1,M>0,N>0);
(4)仿照(3)的证明,你能证明下面的一般性结论吗?logaM-logaN=loga![]() (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)
(5)计算:log34+log39-log312的值为______.
【答案】(1)2,4,6;(2)log24+log216=log264;(4)见解析;(5)1
【解析】
(1)直接根据定义计算即可;
(2)根据计算的值可得等量关系式:log24+log216=log264;
(4)根据同底数幂的除法可得结论;
(5)直接运用(3)(4)中得出的公式即可将原式化简为:log3![]() ,再利用阅读材料中的定义计算即可.
,再利用阅读材料中的定义计算即可.
解:(1)log24=log222=2,log216=log224=4,log264=log226=6;
故答案为:2,4,6;
(2)通过观察(1)中三数log24、log216、log264之间满足的关系式是:log24+log216=log264;
(4)证明:设logaM=m,logaN=n,
由对数的定义得:am=M,an=N,
∴am÷an=am-n=![]() ,
,
∴loga![]() =m-n,
=m-n,
又∵logaM=m,logaN=n,
∴logaM-logaN=loga![]() (a>0且a≠1,M>0,N>0)
(a>0且a≠1,M>0,N>0)
(4)log34+log39-log312,
=log3![]() ,
,
=log33,
=1.
故答案为:1.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A在第一象限,AB⊥x轴于B.AC⊥y轴于C,A(4a,3a),且四边形ABOC的面积为48.
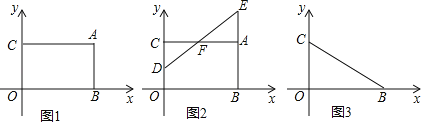
(1)如图1,直接写出点A的坐标;
(2)如图2,点D从O出发以每秒1个单位的速度沿y轴正半轴运动,同时点E从A出发,以每秒2个单位的速度沿射线BA运动,DE交线段AC于F,设运动的时间为t,当S△AEF<S△CDF时,求t的取值范围;
(3)如图3,将线段BC平移,使点B的对应点M恰好落在y轴负半轴上,点C的对应点为N,连BN交y轴轴于P,当OM=3OP时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=4,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于4,则α=_____.
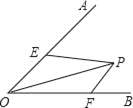
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
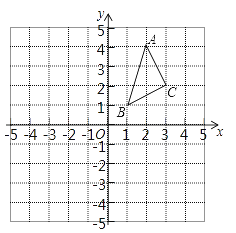
(1)①作出△ABC向左平移4个单位长度后得到的△A1B1C1, 并写出点C1的坐标;
②作出△ABC关于原点O对称的△A2B2C2, 并写出点C2的坐标;
(2)已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为(-4,-2),请直接写出直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统的端午节即将来临,某企业接到一批粽子生产任务,约定这批粽子的出厂价为每只4元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足如下关系:
y=![]()
(1)李明第几天生产的粽子数量为280只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价-成本)
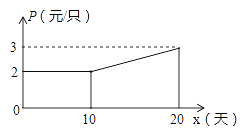
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…嘉琪依次在小球上标上数字1,2,3,4,5,6,…,则从左往右第100个黄球上所标的数字为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
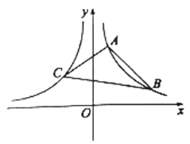
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
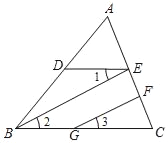
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com