练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，自左向右，水平摆放一组小球，按照以下规律排列，如：红球，黄球，绿球，红球，黄球，绿球，…嘉琪依次在小球上标上数字1，2，3，4，5，6，…，则从左往右第100个黄球上所标的数字为__________．

    【答案】299

    【解析】

    由图可知，每三个球一个循环，左边第一个黄球的数字是2，第二个黄球的数字是2+3=5，第三个黄球的数字是2+3×2=8，…第n个黄球的数字为2+3×(n-1)=3n-1，据此即可解答本题．

    解：由题意得，每三个球一个循环，

    左边第一个黄球的数字是2，

    左边第二个黄球的数字是2+3=5，

    左边第三个黄球的数字是2+3×2=8，

    …

    左边第n个黄球的数字为2+3×(n-1)=3n-1，

    ∴从左往右第100个黄球上所标的数字为：．

    故答案为：299．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知，两点在数轴上，点表示的数为-10，，点以每秒3个单位长度的速度从点向右运动．点以每秒2个单位长度的速度从点向右运动（点、同时出发）

    （1）请你写出数轴上点对应的数；

    （2）当运动的时间为3秒时，请你求出此时点、在数轴上对应的数，并求出、之间的距离；

    （3）经过几秒，点、点分别到原点的距离相等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是等腰直角三角形，∠ACB=90°，AC=BC=2，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是________.

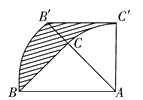
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料并解决后面的问题

    材料：对数的创始人是苏格兰数学家纳皮尔（J．Npler，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler，1707--1783）才发现指数与对数之间的联系，我们知道，n个相同的因数a相乘aa…，a记为an，如23=8，此时，3叫做以2为底8的对数，记为log28，即log28=3一般地若an=b（a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为logab，即logab=n．如34=81，则4叫做以3为底81的对数，记为log381，即log381=4．

    （1）计算下列各对数的值：log24=______，log216=______，log264=______；

    （2）通过观察（1）中三数log24、log216、log264之间满足的关系式是______；

    （3）拓展延伸：下面这个一股性的结论成立吗？我们来证明logaM+logaN=logaMN（a＞0且a≠1，M＞0，N＞0）

    证明：设logaM=m，logaN=n，

    由对数的定义得：am=M，an=N，

    ∴aman=am+n=MN，

    ∴logaMN=m+n，

    又∵logaM=m，logaN=n，

    ∴logaM+logaN=logaMN（a＞0且a≠1，M＞0，N＞0）；

    （4）仿照（3）的证明，你能证明下面的一般性结论吗？logaM-logaN=loga（a＞0且a≠1，M＞0，N＞0）

    （5）计算：log34+log39-log312的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在四边形ABCD中，AC⊥BD于点E，AB=AC=BD，点M为BC中点，N为线段AM上的点，且MB=MN.

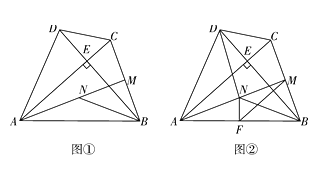
    （1）求证：BN平分∠ABE；

    （2）若BD=1，连结DN，当四边形DNBC为平行四边形时，求线段BC的长；

    （3）如图②，若点F为AB的中点，连结FN、FM，求证：△MFN∽△BDC.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元.

    (1)第一批饮料进货单价多少元？

    (2)若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，AB＝4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF＝FH，②∠HAE＝45°，③BD＝2FG，④△CEH的周长为定值，其中正确的结论有（　　）

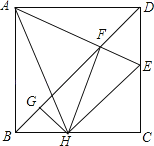
    A. ①②③ B. ①②④ C. ①③④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点在数轴上分别表示有理数，两点之间的距离表示为，在数轴上A、B两点之间的距离．

    利用数形结合思想回答下列问题：

    (1)数轴上表示-2和1的两点之间的距离是______．

    (2)数轴上表示和-1的两点之间的距离表示为______．

    (3)在数轴上点表示数，点表示数，点表示数，且满足，若是数轴上任意一点，点表示的数是，当时，的值为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方体的底面是边长为2cm的正方形，高是6cm．

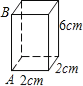
    （1）如果用一根细线从点A开始经过4个侧面围绕一圈到达点B．那么所用的细线最短长度是多少厘米？

    （2）如果从A点开始经过4个侧面缠绕2圈到达点B，那么所用细线最短长度是多少厘米？

    查看答案和解析>>

    同步练习册答案