
【题目】如图,长方体的底面是边长为2cm的正方形,高是6cm.
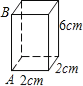
(1)如果用一根细线从点A开始经过4个侧面围绕一圈到达点B.那么所用的细线最短长度是多少厘米?
(2)如果从A点开始经过4个侧面缠绕2圈到达点B,那么所用细线最短长度是多少厘米?
【答案】(1)所用的细线最短长度是10cm;;(2)所用细线最短长度是2![]() cm.
cm.
【解析】
(1)把长方体沿AB边剪开,再根据勾股定理进行解答即可;
(2)如果从点如果从点A开始经过4个侧面缠绕2圈到达点B,相当于直角三角形的两条直角边分别是8和3,再根据勾股定理求出斜边长即可.
(1)如图1所示:
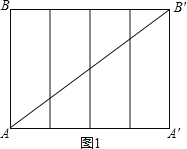
连接AB′,则AB′即为所用的最短细线长,
AA′=8cm,A′B′=AB=6cm,
由勾股定理得:AB′2=AA′2+A′B′2=62+82=100,
则AB′=10cm,
答:所用的细线最短长度是10cm;
(2)将长方体的侧面沿AB展开,取A′B′的中点C,连接BC,AC,则AC+BC为所求的最短细线长,
AC2=AA′2+A′C′2,AC=![]() cm,
cm,
AC2=BB′2+CB′2=73,
BC=![]() (cm),
(cm),
AC+BC=2![]() (cm),
(cm),
答:所用细线最短长度是2![]() cm.
cm.



科目:初中数学 来源: 题型:
【题目】如图,自左向右,水平摆放一组小球,按照以下规律排列,如:红球,黄球,绿球,红球,黄球,绿球,…嘉琪依次在小球上标上数字1,2,3,4,5,6,…,则从左往右第100个黄球上所标的数字为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
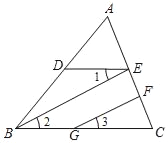
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
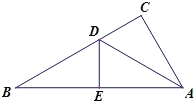
【题目】如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
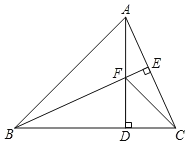
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=3![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
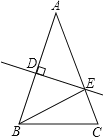
【题目】如图,在△ABC中,AB=AC=30cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=70°,则∠BEC=_____;(2)若BC=20cm,则△BCE的周长是_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列表格:请你结合该表格及相关知识,求出b、c的值.即b=_________,c=___________。
列举 | 猜想 |
3、4、5 | 32=4+5 |
5、12、13 | 52=12+13 |
7、24、25 | 72=24+25 |
…… | …… |
13、b、c | 132=b+c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com