
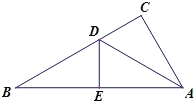
【题目】如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
【答案】(1)△ABC是直角三角形;(2)CD长为3.
【解析】
(1)利用勾股定理的逆定理判断得出即可;
(2)设CD=x,则DE=x,BD=8﹣x,在Rt△BDE中,根据DE2+BE2=BD2列出方程,进而求出即可.
(1)△ABC是直角三角形.
理由:在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8﹣x.
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+(10-6)2=(8﹣x)2,
∴x2+16=64﹣16x+x2,
∴x=3,即CD长为3.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
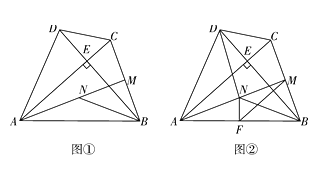
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
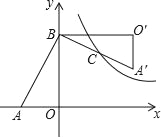
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
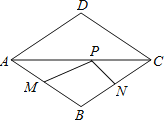
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的底面是边长为2cm的正方形,高是6cm.
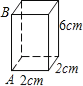
(1)如果用一根细线从点A开始经过4个侧面围绕一圈到达点B.那么所用的细线最短长度是多少厘米?
(2)如果从A点开始经过4个侧面缠绕2圈到达点B,那么所用细线最短长度是多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
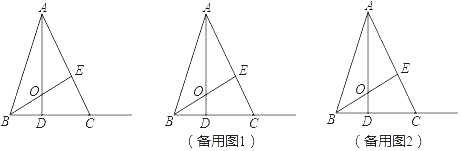
【题目】如图,在△ABC中,BC=5,高AD、BE相交于点O,BD=![]() CD,且AE=BE.
CD,且AE=BE.
(1)求线段AO的长;
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出相应的t的取值范围;
(3)在(2)的条件下,点F是直线AC上的一点且CF=BO.是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请直接写出符合条件的t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
善于思考的小聪在解方程组 时,发现方程组①和②之间存在一定关系,他的解法如下:
时,发现方程组①和②之间存在一定关系,他的解法如下:
解:将方程②变形为:2x-3y-2y=5③,
把方程①代入方程③得:3-2y=5,
解得y=-1.
把y=-1代入方程①得x=0.
∴原方程组的解为![]() .
.
小聪的这种解法叫“整体换元”法.请用“整体换元”法完成下列问题:
(1)解方程组: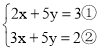 ;
;
①把方程①代入方程②,则方程②变为______;
②原方程组的解为______.
(2)解方程组:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )

A. 10B. 9C. 8D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com