
【题目】如图1,△ACB和△DCE均为等边三角形,点A. D.E在同一直线上,连接BE.
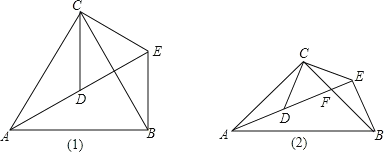
填空:(1),①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 ;
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,且交BC于点F,连接BE.若∠CAF=∠BAF,BE=2,试求AF的长.
【答案】(1)①60°;②AD=BE;(2)4.
【解析】
(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数;
(2)仿照(1)中的解法可求出∠AEB的度数,延长BE交AC的延长线于点G,推出△ACF≌△BCG,根据全等三角形的性质得到AF=BG,由于∠CAF=∠BAF,∠AEB=90°,求得E是BG的中点,即可求出AF=4.
(1)①如图1,
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
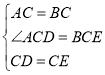 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE;
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
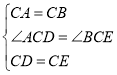 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC∠CED=90°;
延长BE交AC的延长线于点G,
在△ACF和△BCG中,
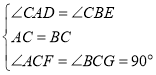 ,
,
∴△ACF≌△BCG,
∴AF=BG,
∵∠CAF=∠BAF,∠AEB=90°,
∴E是BG的中点,
∵BE=2,
∴AF=4.


科目:初中数学 来源: 题型:
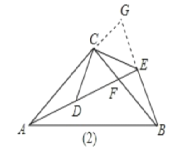
【题目】如图,都是由同样大小的⊙按一定规律所组成的,其中第一个图形有5个⊙,第二个图形一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第2019个图形中基本图形的个数为( )
A.6056B.6057C.6058D.6059
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )

A. △EBD是等腰三角形,EB=ED B. 折叠后∠ABE和∠C′BD一定相等
C. 折叠后得到的图形是轴对称图形 D. △EBA和△EDC′一定是全等三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,
表示的数为-10,![]() ,点
,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)请你写出数轴上点![]() 对应的数;
对应的数;
(2)当运动的时间为3秒时,请你求出此时点![]() 、
、![]() 在数轴上对应的数,并求出
在数轴上对应的数,并求出![]() 、
、![]() 之间的距离;
之间的距离;
(3)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
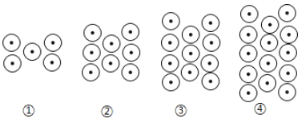
【题目】在平面直角坐标系中,O为坐标原点,点A(8,0)动点P从A出发以每秒2个单位长度的速度沿线段AO向终点O运动,同时动点Q从O出发以相同速度沿y轴正半轴运动,点P到达点O,两点同时停止运动.
(1)当t= 时,∠OPQ=45°;
(2)如图2,以PQ为斜边在第一象限作等腰Rt△PQM,求M点坐标;
(3)在(2)的条件下,点R位x轴负半轴上一点,且![]() ,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:(1)AD上任意一点到点C、D的距离相等;(2)AD上任意一点到AB、AC的距离相等;(3)AD⊥BC且BD=CD;(4)∠BDE=∠CDF,其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
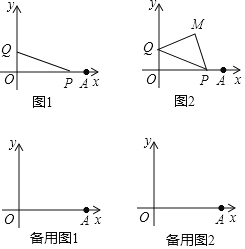
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC
(1)填空:如图1,∠B= °,∠C= °;
(2)如图2,若M为线段BC上的点,过M作MH⊥AD,交AD的延长线于点H,分别交直线AB、AC与点N、E.
①求证:△ANE是等腰三角形;
②线段BN、CE、CD之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com