
分析 由在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分成12cm和15cm两部分,可得|AB-BC|=15-12=3(cm),AB+BC+AC=2AB+BC=12+15=27cm,然后分别从AB>BC与AB<BC去分析求解即可求得答案.
解答 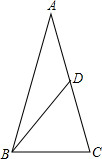 解:如图,∵AB=AC,BD是AC边上的中线,
解:如图,∵AB=AC,BD是AC边上的中线,
即AD=CD,
∴|(AB+AD)-(BC+CD)|=|AB-BC|=15-12=3(cm),AB+BC+AC=2AB+BC=12+15=27cm,
若AB>BC,则AB-BC=3cm,
又∵2AB+BC=27cm,
联立方程组并求解得:AB=10cm,BC=7cm,
10cm、10cm、7cm三边能够组成三角形;
若AB<BC,则BC-AB=3cm,
又∵2AB+BC=27cm,
联立方程组并求解得:AB=8cm,BC=11cm,
8cm、8cm、11cm三边能够组成三角形;
∴三角形的各边长为10cm、10cm、7cm或8cm、8cm、11cm.
点评 此题考查了等腰三角形的性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
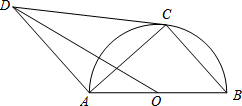 如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B,连接OD.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,AD∥BC,且∠DCA=∠B,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
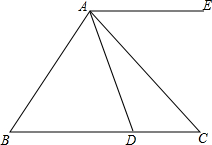 如图,已知在△ABC中,∠ABC-∠ACB=20°,∠ACB的度数是∠BAC度数的$\frac{1}{2}$.
如图,已知在△ABC中,∠ABC-∠ACB=20°,∠ACB的度数是∠BAC度数的$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000.
y与x的函数图象如图所示,当0≤x≤100时,y与x的函数关系式为y=100x;当x>100时,y与x的函数关系式为y=60x+4000.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com