
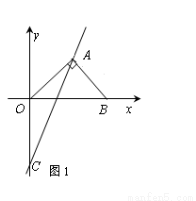
��ͼ1����ƽ��ֱ������ϵ�У�����Rt��AOB��б��OB��x���ϣ�ֱ��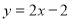 ��������Rt��AOB��ֱ�Ƕ���A����y����C�㣮
��������Rt��AOB��ֱ�Ƕ���A����y����C�㣮
(1) ���A���ꣻ
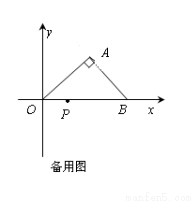
(2)����PΪx����һ���㣮��Q�������ǣ�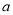 ��
��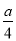 ������PAQ���Ե�AΪֱ�Ƕ���ĵ��������Σ����
������PAQ���Ե�AΪֱ�Ƕ���ĵ��������Σ����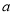 ��ֵ��д����Q�����꣮
��ֵ��д����Q�����꣮
��3����(2)�������£���D������ƽ��������һ�㣬ʹ��A��P��Q��D�պ��ܹ���ƽ���ı��Σ���ֱ��д�����������ĵ�D������
��
��1��A��2��2������2��a=4��Q��4��1����3��D�����������1��1������5��3������3����2����
��������
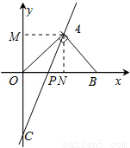
�����������1������A�ֱ���AM��y����M�㣬AN��x����N�㣬����ֱ�������ε����ʿ����A������Ϊ��a��a������Ϊ��A��ֱ��y=2x��2�ϣ�����A������������ʽ�������a��ֵ�������õ�A�����꣮
��2������AQ����A����AP��AQ��x����P�㣮��ASA��֤��AOP�ա�ABQ���ó���AOP=��ABQ=45���Ӷ����QB��OB������B�㡢Q�����������ȵó������
��3����Ϊ��D��A��P��Q���㹹��ƽ���ı��Σ��������������ۣ���ΪA��2��2����P����1��0����Q��4��1��������ƽ���ı��εĶԱ߷ֱ�ƽ������ȣ�
��QD��BA������������ĵ�D������ֱ���D1��5��3����D2��3����2������PD��QA������������ĵ�D������ֱ���D2��3����2����D3����1��1����
�����������1������A�ֱ���AM��y����M�㣬AN��x����N�㣬
�ߡ�AOB�ǵ���ֱ�������Σ�
��AM=AN��
���A��������a��a����
����A��ֱ��y=2x��2�ϣ�
��a=2a��2��
���a=2��
��A��2��2��
��2������AQ����A����AP��AQ��x����P�㣬
����APQΪ����ֱ�������Σ�
�ߡ�OAB=��PAQ=90��
���OAB����PAB=��PAQ����PAB��
���OAP=��BAQ��
����APO����ABQ��

���APO�ա�ABQ��SAS����
���AOP=��ABO=45��
��QB��OB
��A��2��2��
��B��4��0��
��Q��������ǣ�a�� ����
����
��a=4��
��Q��4��1����
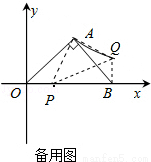
��3���ڣ�2���������£���D������ƽ��������һ�㣬ʹ��A��P��Q��D�պ��ܹ���ƽ���ı��Σ���D�������Ϊ����1��1������5��3������3����2����
���㣺һ�κ����ۺ�����


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�����а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
��֪n����������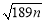 ����������n����Сֵ�� ��
����������n����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�Ͼ��ߴ����꼶��ѧ�����м����ѧ�Ծ��������棩 ���ͣ�ѡ����
������ʽ��ȷ������ ����
A�� B��
B��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�˻��а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ�����ܳ�Ϊ10 cm����ABCD�У�AB��AD��AC��BD�ཻ�ڵ�O��OE��BD��AD�ڵ�E������BE������ABE���ܳ�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�˻��а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
����������ȷ����( )
A��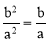 B��
B��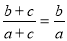 C��
C��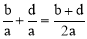 D��
D��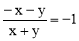
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭�������а��꼶��ѧ�����п�����ѧ���������棩 ���ͣ������
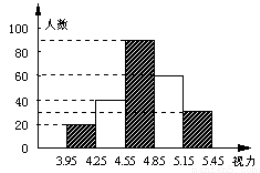
������������״���ܵ�ȫ���Ĺ㷺��ע��ij���йز��Ŷ�ȫ��3��������������״��������һ�γ������飬��ͼ�������������ݻ��Ƶ�Ƶ���ֲ�ֱ��ͼ(�����εĸ߱�ʾ��������)������ͼ�����ṩ����Ϣ���ش�����������
��1�����ε��鹲����� ��ѧ����ռ���г����������İٷֱ��� ��
��2�����������С���Ƶ��֮���� ��
��3�����������4.9����(��4.9)������������ȫ���� �������������������� ���������ĺϸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭�������а��꼶��ѧ�����п�����ѧ���������棩 ���ͣ������
��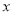 ��
��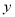 ����
����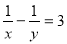 �����ʽ
�����ʽ 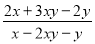 ��ֵΪ .
��ֵΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭������ǰ����ѧ���꼶3�½���ϰ��ѧ�Ծ��������棩 ���ͣ������
��֪:��ͼ������ABCD,E��BC���е�,F��AB��,��BF= ,����EF��DE��λ�ù�ϵ,��˵������.
,����EF��DE��λ�ù�ϵ,��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭�����˺���ѧ�����꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ���� �� ��
A����AB=BCʱ���������� B������ABC=90��ʱ�����Ǿ���
C����AC=BDʱ������������ D����AC��BDʱ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com