
【题目】已知菱形ABCD,对角线交点为O,延长CD至E且CD=DE.下列判断正确个数是( )
(1)∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO.
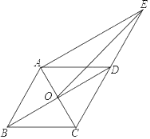
A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
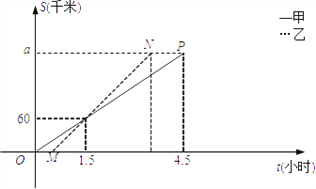
【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;②请问甲车在离B地多远处与返程中的乙车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )
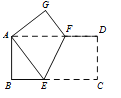
A. AF=AE B. △ABE≌△AGF C. EF=![]() D. AF=EF
D. AF=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=10°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1 P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2 P3;……
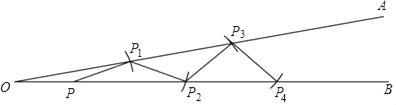
请按照上面的要求继续操作并探究:
∠P3 P2 P4=_____°;按照上面的要求一直画下去,得到点Pn,若之后就不能再画出符合要求点Pn+1了,则n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
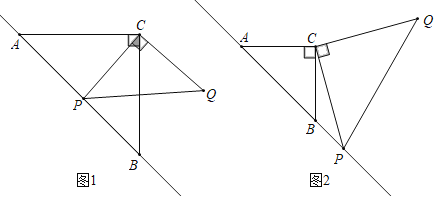
【题目】已知△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
(1)如图1,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,求线段PC的长.
,求线段PC的长.
(2)如图2,若点P在AB的延长线上,猜想PA2、PB2、PC2之间的数量关系,并证明.
(3)若动点P满足![]() ,则
,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2-4x+3的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,抛物线的对称轴与x轴交于点D.
(1)求点A,点B和点D的坐标;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;
(3)若动点M从点A出发,以每秒1个单位长度的速度沿AB向点B运动,同时另一个动点N从点D出发,以每秒2个单位长度的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,MNB的面积最大,试求出最大面积.

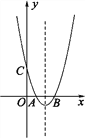 (备用图)
(备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批自行车. 男式自行车价格为![]() 元/辆,女式自行车价格为
元/辆,女式自行车价格为![]() 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多![]() 辆,设购进女式自行车
辆,设购进女式自行车![]() 辆,购置总费用为
辆,购置总费用为![]() 元.
元.
(1)求购置总费用![]() (元)与女式单车
(元)与女式单车![]() (辆)之间的函数关系式;
(辆)之间的函数关系式;
(2)若两种自行车至少需要购置![]() 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过![]() 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店出售A、B两种商品,一月份这两种商品的利润都是10万元,后因某种原因确定增加出售A种商品的数量,使A种商品每月利润的增长率都为a,同时减少B种商品的数量,使B种商品每月利润减少的百分率也都是a,(1)分别求出二月份出售A和B两种商品的利润是多少万元?(2)求出三月份出售A、B两种商品的总利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com