
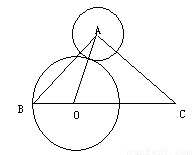
如图,在△ABC中∠BAC=90°,AB=AC=2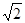 ,圆A的半径1,点O在BC边上运动(与点B/C不重合),设BO=X,△AOC的面积是y.
,圆A的半径1,点O在BC边上运动(与点B/C不重合),设BO=X,△AOC的面积是y.
⑴求y关于x的函数关系式及自变量的取值范围;
⑵以点O位圆心,BO为半径作圆O,求当○O与○A相切时,△AOC的面积.
(1)∵∠BAC=90°,AB=AC=2  ,
,
由勾股定理知BC= =4,且∠B=∠C,
=4,且∠B=∠C,
作AM⊥BC,
则∠BAM=45°,BM=CM=2=AM,
∵BO=x,则OC=4﹣x,
∴S△AOC= OC•AM=
OC•AM= ×(4﹣x)×2=4﹣x,
×(4﹣x)×2=4﹣x,
即y=4﹣x (0<x<4);
(2)①作AD⊥BC于点D,

∵△ABC为等腰直角三角形,BC=4,
∴AD为BC边上的中线,
∴AD= =2,
=2,
∴S△AOC= ,
,
∵BO=x,△AOC的面积为y,
∴y=4﹣x(0<x<4),
②过O点作OE⊥AB交AB于E,

∵⊙A的半径为1,OB=x,
当两圆外切时,
∴OA=1+x,
∵△ABC为等腰直角三角形,
∴∠B=45°,
∴BE=OE= ,
,
∴在△AEO中,AO2=AE2+OE2=(AB﹣BE)2+OE2,
∴(1+x)2=(2 ﹣
﹣ )2+(
)2+( )2,
)2,
∴x= ,
,
∵△AOC面积=y=4﹣x,
∴△AOC面积= ;
;
当两圆内切时,

∴OA=x﹣1,
∵AO2=AE2+OE2=(AB﹣BE)2+OE2,
∴(x﹣1)2=(2 ﹣
﹣ )2+(
)2+( )2,
)2,
∴x= ,
,
∴△AOC面积=y=4﹣x=4﹣ =
= ,
,
∴△AOC面积为 或
或 .
.
【解析】(1)由∠BAC=90°,AB=AC=2  ,根据勾股定理即可求得BC,且∠B=∠C,然后作AM⊥BC,由S△AOC=
,根据勾股定理即可求得BC,且∠B=∠C,然后作AM⊥BC,由S△AOC= OC•AM,即可求得y关于x的函数解析式;
OC•AM,即可求得y关于x的函数解析式;
(2)由⊙O与⊙A外切或内切,即可求得ON的值,继而求得△AOC的面积.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com