
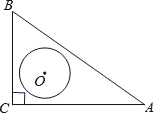
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是_____.
【答案】1≤r≤![]()
【解析】分析:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,根据题意得出四边形OECF是正方形,得出OF=CF,由勾股定理得出AB=![]() =5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
=5,由内心的性质得出CF=OF=1,AF=AC﹣CF=3,由勾股定理求出OA,由直线与圆的位置关系,即可得出结果.
详解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示
则四边形OECF是正方形,∴OF=CF=OE=CE.
∵∠C=90°,AC=4,BC=3,∴AB=![]() =5.
=5.
∵O是△ABC的内心,∴CE=CF=OF=OE=![]() (AC+BC﹣AB)=1,∴AF=AC﹣CF=3,BE=BC﹣CE=2,∴OA=
(AC+BC﹣AB)=1,∴AF=AC﹣CF=3,BE=BC﹣CE=2,∴OA=![]() =
=![]() =
=![]() ,OB=
,OB=![]() =
=![]() =
=![]() ,当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
,当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当![]() <r≤
<r≤![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤![]() ;
;
故答案为:1≤r≤![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】绿水青山就是金山银山,国家倡导全民植树。在今年3月12日植树节当天,某校七年级一班48名学生全部参加了植树活动,男生每人栽种4株,女生每人栽种3株,全班共栽种170株。
(1)该班男、女生各为多少人?
(2)学校选择购买甲、乙两种树苗,甲树苗![]() ,乙树苗
,乙树苗![]() .如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
.如果要使购买树苗的钱不超过1200元,那么最多可以购买甲树苗多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①BE=DF;②∠AEB=75°;③CE=2;④S正方形ABCD=2+![]() ,其中正确答案是( )
,其中正确答案是( )

A.①②B.②③C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
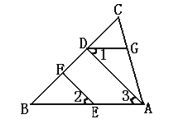
【题目】如图,EF∥AD,∠1=∠2,∠BAC=72 o,求∠AGD的度数.
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3
所以AB∥ ( )
所以∠BAC+ =180 o( )
因为∠BAC=72 o
所以∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
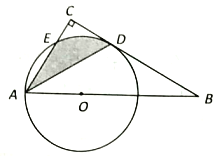
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com