
 如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.
如图,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一直线上,且AB=$\sqrt{3}$,BC=1,连结BF,分别交AC,DC,DE于点P,Q,R.分析 (1)已知三个全等的等腰三角形,以及边长,所以可求得各线段的长,即可求得线段的比值,由公共角即可证得△BFG∽△FEG;
(2)利用△BPC~△BFG求得PC的长,进而可知AP的长,即可得答案.
(3)可以提问求证:∠PCB=∠REC,这个问题只需要运用两直线平行,同位角相等进行解答.此题为发散性题型,不唯一.
解答 解:(1)据题意知BC=CE=EG=1,BG=3,FG=AB=$\sqrt{3}$,
在△BFG和△FEG中,
∵$\frac{FG}{EG}$=$\frac{BG}{FG}$=$\sqrt{3}$,∠G=∠G
∴△BFG∽△FEG;
(2)∵△ABC≌△FEG,
∴∠ACB=∠G,
∴PC∥FG,
∴△BPC~△BFG,
∴$\frac{PC}{BC}$=$\frac{FG}{BG}$,即 $\frac{PC}{1}$=$\frac{\sqrt{3}}{3}$,
解得:PC=$\frac{\sqrt{3}}{3}$,
∵AC=AB=$\sqrt{3}$,
∴AP=AC-PC=$\frac{2\sqrt{3}}{3}$,
∴$\frac{AP}{PC}$=$\frac{\frac{2\sqrt{3}}{3}}{\frac{\sqrt{3}}{3}}$=2.
(3)①求证:∠PCB=∠REB,②求证:PC∥RE,答案不唯一.
证明:∵△ABC≌△DCE,
∴∠PCB=∠REB,
∴PC∥RE.
点评 本题主要考查了相似三角形的判定与性质及全等三角形、等腰三角形的性质运用,熟练掌握相似三角形的判定与性质是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 3000x2=7500 | B. | 3000(1+x)2=7500 | ||
| C. | 3000(1+x%)2=7500 | D. | 3000(1+x)+3000(1+x)2=7500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
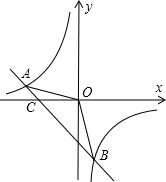 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13cm,12cm,20cm | B. | 8cm,7cm,15cm | C. | 5cm,5cm,11cm | D. | 3cm,4cm,8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
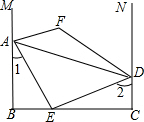 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )
如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F.∠F的度数为( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com