
分析 设$\frac{531}{135}+\frac{579}{357}+\frac{753}{975}+\frac{135}{531}$=a,则$\frac{531}{135}+\frac{579}{357}+\frac{753}{975}$=a-$\frac{135}{531}$,$\frac{597}{357}+\frac{753}{975}+\frac{135}{531}$=a-$\frac{531}{135}$,进一步代入求得答案即可.
解答 解:设$\frac{531}{135}+\frac{579}{357}+\frac{753}{975}+\frac{135}{531}$=a,则$\frac{531}{135}+\frac{579}{357}+\frac{753}{975}$=a-$\frac{135}{531}$,$\frac{597}{357}+\frac{753}{975}+\frac{135}{531}$=a-$\frac{531}{135}$,
原式=(a-$\frac{135}{531}$)(a-$\frac{531}{135}$)-a×($\frac{579}{357}+\frac{753}{975}$)
=a2-($\frac{135}{531}$+$\frac{531}{135}$)a+1-a×($\frac{579}{357}+\frac{753}{975}$)
=a2-($\frac{531}{135}+\frac{579}{357}+\frac{753}{975}+\frac{135}{531}$)a+1
=a2-a2+1
=1.
点评 此题考查有理数的混合运算,抓住数字的特点,利用整体思想解决问题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
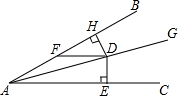 如图所示.已知∠BAC=30°,AD平分∠BAC.DE⊥AC于点E.DH⊥AB于点H,DF∥AC,交AB于点F.若DF=10cm.求DE的长.
如图所示.已知∠BAC=30°,AD平分∠BAC.DE⊥AC于点E.DH⊥AB于点H,DF∥AC,交AB于点F.若DF=10cm.求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com