
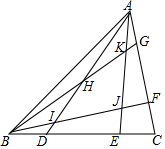
 如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE=$\frac{1}{4}$BC,CF=AG=$\frac{1}{4}$AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ.
如图,在△ABC中,BC边上依次有B、D、E、C,AC边上依次有A、G、F,满足BD=CE=$\frac{1}{4}$BC,CF=AG=$\frac{1}{4}$AC,BF交AE于点J,交AD于I,BG交AE于点K,交AD于点H,且S△ABC=1,求S四边形KHIJ. 分析 作平行线GP和FM,根据平行线分线段成比例定理列比例式得:$\frac{GH}{BH}=\frac{3}{4}$,$\frac{GQ}{BE}=\frac{GK}{BK}$=$\frac{1}{12}$,从而得:BH:HK:KG=52:32:7,BI:IJ:JF=20:32:13,由同高三角形面积的比等于对应底边的比,可以得出S△ABF=$\frac{3}{4}$,S△ABG=$\frac{1}{4}$,S△AIJ=$\frac{32}{65}$S△ABF=$\frac{32}{65}$×$\frac{3}{4}$=$\frac{24}{65}$,S△AHK=$\frac{32}{91}$S△ABG=$\frac{32}{91}$×$\frac{1}{4}$=$\frac{8}{91}$,作差可得S四边形KHIJ.
解答 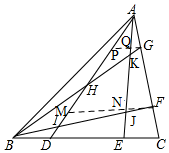 解:过G作GP∥BC,交AD于P,AE于Q,则$\frac{PG}{CD}=\frac{AG}{AC}$=$\frac{1}{4}$,
解:过G作GP∥BC,交AD于P,AE于Q,则$\frac{PG}{CD}=\frac{AG}{AC}$=$\frac{1}{4}$,
∵BD=$\frac{1}{4}$BC,
∴$\frac{PG}{3BD}$=$\frac{1}{4}$,
∴$\frac{PG}{BD}=\frac{3}{4}$,
∵$\frac{PG}{BD}=\frac{GH}{BH}$,
∴$\frac{GH}{BH}=\frac{3}{4}$,
同理可得:$\frac{GQ}{EC}=\frac{AG}{AC}$=$\frac{1}{4}$,
即$\frac{GQ}{\frac{1}{3}BE}$=$\frac{1}{4}$,
∴$\frac{GQ}{BE}=\frac{1}{12}$,
∴$\frac{GQ}{BE}=\frac{GK}{BK}$=$\frac{1}{12}$,
∴BH:HK:KG=52:32:7,
过F作FM∥BC,交AD于M,AE于N,
同理得:BI:IJ:JF=20:32:13,
∵S△ABC=1,
∴S△ABF=$\frac{3}{4}$,S△ABG=$\frac{1}{4}$,
∴S△AIJ=$\frac{32}{65}$S△ABF=$\frac{32}{65}$×$\frac{3}{4}$=$\frac{24}{65}$,
S△AHK=$\frac{32}{91}$S△ABG=$\frac{32}{91}$×$\frac{1}{4}$=$\frac{8}{91}$,
∴S四边形KHIJ=S△AIJ-S△AHK,
=$\frac{24}{65}$-$\frac{8}{91}$,
=$\frac{128}{455}$.
点评 本题计算三角形和多边形面积,考查了平行线分线段成比例定理、同高三角形面积的关系,作好本题要从以下几点入手:①作平行线,②根据平行线分线段成比例定理得线段的比,③根据边的比得出面积的比.


科目:初中数学 来源: 题型:选择题
| A. | 40cm | B. | 30cm | C. | 20cm | D. | 17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
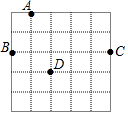 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com