
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
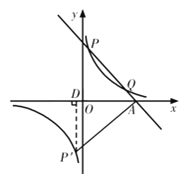
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
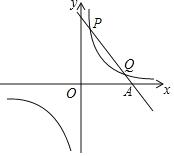
【答案】(1) 反比例函数的表达式为y=![]() ,一次函数的表达式为y=﹣2x+9;(2) (-
,一次函数的表达式为y=﹣2x+9;(2) (-![]() ,﹣8);(3)
,﹣8);(3) ![]() .
.
【解析】
试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,
∴把点P(![]() ,8)代入y=
,8)代入y=![]() 可得:k2=4,
可得:k2=4,
∴反比例函数的表达式为y=![]() ,
,
∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入y=k1x+b中,
,8),Q (4,1)分别代入y=k1x+b中,
得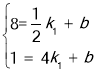 ,
,
解得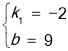 ,
,
∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(-![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(-![]() ,﹣8),
,﹣8),
∴OD=![]() ,P′D=8,
,P′D=8,
∵点A在y=﹣2x+9的图象上,
∴点A(![]() ,0),即OA=
,0),即OA=![]() ,
,
∴DA=5,
∴P′A=![]() ,
,
∴sin∠P′AD=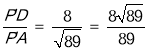 ,
,
∴sin∠P′AO= ![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( ) 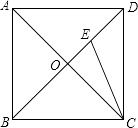
A.22.5°
B.60°
C.67.5°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副”弦图“,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为 . 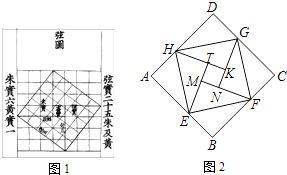
查看答案和解析>>
科目:初中数学 来源: 题型:
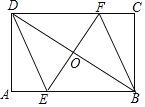
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: 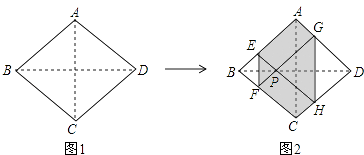
①当x=1时,点P是正方形ABCD的中心;
②当x= ![]() 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是(写出所有正确判断的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com