
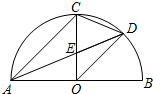
 如图所示,AB是半圆形的直径,半径OC⊥AB于点O,AD平分∠CAB交$\widehat{BC}$于点D,连接CD,OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠COD=∠DAB;④∠COD=∠CDA,其中正确结论的序号是①②④.
如图所示,AB是半圆形的直径,半径OC⊥AB于点O,AD平分∠CAB交$\widehat{BC}$于点D,连接CD,OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠COD=∠DAB;④∠COD=∠CDA,其中正确结论的序号是①②④. 分析 ①根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可;
②过点E作EF⊥AC,根据角平分线上的点到角的两边的距离相等可得OE=EF,再根据直角三角形斜边大于直角边可证;
③根据半径OC⊥AB于点O可知$\widehat{AC}$=$\widehat{BC}$,再由AD平分∠CAB交$\widehat{BC}$于点D可知$\widehat{CD}$=$\widehat{BD}$,故可得出∠COD=2∠DAB;
④直接根据圆周角定理即可得出结论.
解答 解:①∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=$\frac{1}{2}$∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,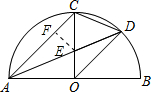
∴①正确.
②过点E作EF⊥AC,
∵OC⊥AB,AD平分∠CAB交弧BC于点D,
∴OE=EF,
在Rt△EFC中,CE>EF,
∴CE>OE,
∴②错误;
③∵半径OC⊥AB于点O,
∴$\widehat{AC}$=$\widehat{BC}$.
∵AD平分∠CAB交$\widehat{BC}$于点D,
∴$\widehat{CD}$=$\widehat{BD}$,
∴∠COD=2∠DAB,故③错误;
④∵由③知,$\widehat{AC}$=2$\widehat{CD}$,
∴∠COD=∠CDA,故④正确.
故答案为:①②④.
点评 此题主要考查圆心角、弧、弦的关系,圆周角定理,等腰三角形的性质,三角形内角和定理等知识点的灵活运用,此题步骤繁琐,但相对而言,难易程度适中.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:填空题
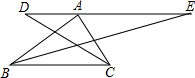 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com