
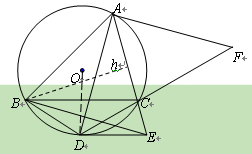
(11·珠海)(本题满分9分)已知:如图,锐角△ABC内接于⊙O,∠ABC=45°;
点D是![]() 上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
上一点,过点D的切线DE交AC的延长线于点E,且DE∥BC;连结AD、BD、
BE,AD的垂线AF与DC的延长线交于点F.
(1)求证:△ABD∽△ADE;
(2)记△DAF、△BAE的面积分别为S△DAF、S△BAE,求证:S△DAF>S△BAE.

证明:(1)连结OD. ……………………1分
∵DE是⊙O的切线,
∴OD⊥DE.
又∵DE∥BC,
∴OD⊥BC.
∴=. ……………………2分
∴∠BAD=∠EAD.
∵∠BDA=∠BCA,DE∥BC,
∴∠BDA=∠DEA.
∴∠BAD=∠EAD,
∴△ABD∽△ADE. ……………………5分
(2)由(1)得=,即AD2=AB·AE ……………………6分
设在△ABE中,AE边上的高为h,则:
∴S△ABE= h·AE,且h<AB.
由∠ABC=45°,AD⊥AF可推得△ADF为等腰直角三角形
∴S△DAF= AD2. ……………………8分
∴S△DAF=S△BAE
∴△DAF>△BAE.
解析:略


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
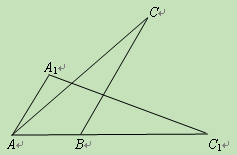
(11·珠海)(本题满分7分)如图,将一个钝角△ABC(其中∠ABC=120°)绕
点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·珠海)(本题满分7分)如图,Rt△OAB中,∠OAB=90°,O为坐标原点,
边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
(11·珠海)(本题满分7分)某校为庆祝国庆节举办游园活动,小军来到摸球
兑奖活动场地,李老师对小军说:“这里有A、B两个盒子,里面都装有一些乒乓球,你只
能选择在其中一只盒子中摸球.”获将规则如下:在A盒中有白色乒乓球4个,红色乒乓球
2个,一人只能摸一次且一次摸出一个球,若为红球则可获得玩具熊一个,否则不得奖;在
B盒中有白色乒乓球2个,红色乒乓球2个,一人只能摸一次且一次摸出两个球,若两球均
为红球则可获得玩具熊一个,否则不得奖.请问小军在哪只盒子内摸球获得玩具熊的机会更
大?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com