
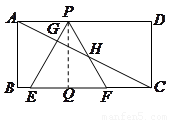
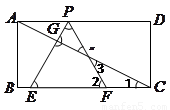
如图,已知矩形ABCD,AB= ,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.
,BC=3,在BC上取两点E、F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE、PF分别交AC于点G、H.

(1)求△PEF的边长;
(2)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有什么数量关系?并证明你猜想的结论.
(1)2(2)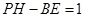 ,证明见解析
,证明见解析
【解析】解: (1)过 作
作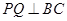 于
于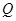
 矩形
矩形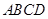
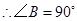 ,即
,即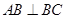 ,又
,又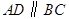
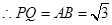 ………………1分
………………1分
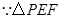 是等边三角形
是等边三角形
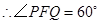
在 中
中

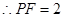
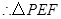 的边长为
的边长为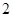 . ……………………………3分
. ……………………………3分
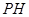 与
与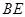 的数量关系是:
的数量关系是: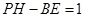 ………4分
………4分
在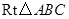 中,
中,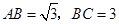
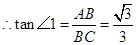
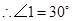 …………………………………5分
…………………………………5分
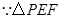 是等边三角形
是等边三角形
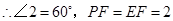 ……………………………6分
……………………………6分

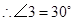
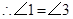
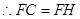 …………………………………………8分
…………………………………………8分
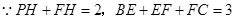
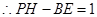 ……………………………………………9分
……………………………………………9分
(1)要求△PEF的边长,需构造直角三角形,那么就过P作PQ⊥BC于Q.利用∠PFQ的正弦值可求出PF,即△PEF的边长;
(2)猜想:PH-BE=1.利用∠ACB的正切值可求出∠ACB的度数,再由∠PFE=60°,可得出△HFC是等腰三角形,因此就有BE+EF+CF=BE+PH+2FH=3.再把其中FH用PH表示,化简即可.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
 如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=
如图,已知矩形DEFG内接于Rt△ABC,D在AB上,E、F在BC上,G在AC上,∠BAC=90°,AB=6cm,AC=8cm,S矩形DEFG=| 45 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).
m/秒的速度移动,如果M、N两点同时出发,移动的时间为x秒(0≤x≤6).查看答案和解析>>
科目:初中数学 来源: 题型:
 点A运动.
点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )
(2012•宁德质检)如图,已知Rt△ABC,∠B=90°,AB=8,BC=6,把斜边AC平均分成n段,以每段为对角线作边与AB、BC平行的小矩形,则这些小矩形的面积和是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<
如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y=mx+n(0<m<n<| 1 |
| 2 |
| 9 |
| 8 |
| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com