解:(1)∵∠BAC=90°,AB=AC=2

,

由勾股定理知BC=

=4,且∠B=∠C,
作AM⊥BC,
则∠BAM=45°,BM=CM=2=AM,
∵BO=x,则OC=4-x,
∴S
△AOC=

OC•AM=

×(4-x)×2=4-x,
即y=4-x (0<x<4);
(2)①作AD⊥BC于点D,

∵△ABC为等腰直角三角形,BC=4,
∴AD为BC边上的中线,
∴AD=

=2,
∴S
△AOC=
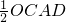
,
∵BO=x,△AOC的面积为y,
∴y=4-x(0<x<4),
②过O点作OE⊥AB交AB于E,

∵⊙A的半径为1,OB=x,
当两圆外切时,
∴OA=1+x,
∵△ABC为等腰直角三角形,
∴∠B=45°,
∴BE=OE=

,
∴在△AEO中,AO
2=AE
2+OE
2=(AB-BE)
2+OE
2,
∴(1+x)
2=(2

-

)
2+(

)
2,

∴x=

,
∵△AOC面积=y=4-x,
∴△AOC面积=
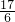
;
当两圆内切时,
∴OA=x-1,
∵AO
2=AE
2+OE
2=(AB-BE)
2+OE
2,
∴(x-1)
2=(2

-

)
2+(

)
2,
∴x=

,
∴△AOC面积=y=4-x=4-

=

,
∴△AOC面积为
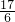
或

.
分析:(1)由∠BAC=90°,AB=AC=2

,根据勾股定理即可求得BC,且∠B=∠C,然后作AM⊥BC,由S
△AOC=

OC•AM,即可求得y关于x的函数解析式;
(2)由⊙O与⊙A外切或内切,即可求得ON的值,继而求得△AOC的面积.
点评:此题考查了相切两圆的性质,三角形面积的求解方法,以及勾股定理的应用等知识.此题综合性较强,难度适中,解题的关键是方程思想与数形结合思想的应用.

 如图,在△ABC中∠BAC=90°,AB=AC=2
如图,在△ABC中∠BAC=90°,AB=AC=2 ,圆A的半径1,点O在BC边上运动(与点B,C不重合),设BO=x,△AOC的面积是y.
,圆A的半径1,点O在BC边上运动(与点B,C不重合),设BO=x,△AOC的面积是y. ,
,
 =4,且∠B=∠C,
=4,且∠B=∠C, OC•AM=
OC•AM= ×(4-x)×2=4-x,
×(4-x)×2=4-x,
 =2,
=2,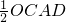 ,
,
 ,
, -
- )2+(
)2+( )2,
)2,
 ,
,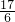 ;
; -
- )2+(
)2+( )2,
)2, ,
, =
= ,
,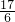 或
或 .
. ,根据勾股定理即可求得BC,且∠B=∠C,然后作AM⊥BC,由S△AOC=
,根据勾股定理即可求得BC,且∠B=∠C,然后作AM⊥BC,由S△AOC= OC•AM,即可求得y关于x的函数解析式;
OC•AM,即可求得y关于x的函数解析式;

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为