




科目:初中数学 来源: 题型:
 (1997•天津)如图,⊙O和⊙O′都经过A、B两点,过B作直线交⊙O于C,交⊙O′于D,G为圆外一点,GC交⊙O于E,GD交⊙O′于F.
(1997•天津)如图,⊙O和⊙O′都经过A、B两点,过B作直线交⊙O于C,交⊙O′于D,G为圆外一点,GC交⊙O于E,GD交⊙O′于F.查看答案和解析>>
科目:初中数学 来源: 题型:
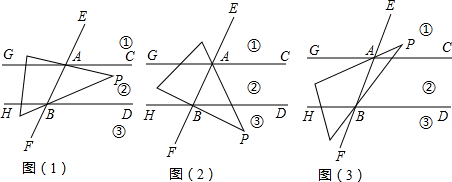
查看答案和解析>>
科目:初中数学 来源: 题型:
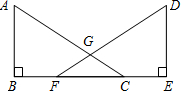 已知,如图,AB=DE,点B、F、C、E在同一直线上,且BF=CE,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E.
已知,如图,AB=DE,点B、F、C、E在同一直线上,且BF=CE,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E.查看答案和解析>>
科目:初中数学 来源:江苏省江阴市南菁中学2012届九年级5月中考适应性训练(二模)数学试题 题型:044
在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B'处(如图2),这样能得到∠B'GC的大小,你知道∠B'GC的大小是多少吗?请写出求解过程.
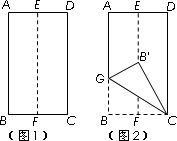
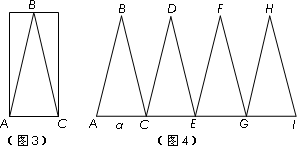
(2)第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15![]() ,请你帮助该小组求出a可能的最大整数值.
,请你帮助该小组求出a可能的最大整数值.
(3)探究活动结束后,老师给大家留下了一道探究题:
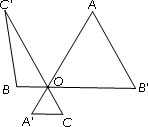
如图5,已知A![]() =B
=B![]() =CC'=2,∠AO
=CC'=2,∠AO![]() =∠BO
=∠BO![]() =∠CO
=∠CO![]() =60°,
=60°,
请利用图形变换探究S△AOB'+S△BOC'+S△COA'与![]() 的大小关系.
的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com