
 如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.
如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.分析 (1)先根据菱形的性质得出∠ABC=120°,AB=CB,再由图形旋转的性质得出EB=FB,根据SAS定理得出△AFB≌△CEB,由全等三角形的性质即可得出结论;
(2)先求出∠ABE的度数,再由等腰三角形的性质求出∠GEB的度数,再由∠AGE=∠ABE+∠GEB即可得出结论.
解答 解:(1)∵四边形ABCD是菱形,∠D=120°,
∴∠ABC=120°,AB=CB.
又∵EB绕着点B逆时针旋转120°到FB,
∴EB=FB,
∴∠FBA+∠ABE=∠ABE+∠EBC=120°,
∴∠FBA=∠EBC,
在△AFB与△CEB中,
∵$\left\{\begin{array}{l}EB=FB\\∠EBC=∠FBA\\ BC=AB\end{array}\right.$,
∴△AFB≌△CEB(SAS),
∴AF=CE;
(2)∵∠ABC=120°,∠EBC=45°,
∴∠ABE=75°.
又∵∠EBF=120°,EB=FB,
∴∠GEB=$\frac{180°-120°}{2}$=30°,
∴∠AGE=∠ABE+∠GEB=75°+30°=105°.
点评 本题考查的是旋转的性质,熟知图形旋转后所得图形与原图形全等是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
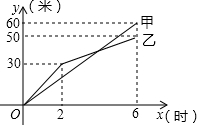 某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:
某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -2 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3a>-3b | B. | 3a-1>3b-1 | C. | 3-a>3-b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com