
 如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在线段AB上,DE⊥CE.
如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在线段AB上,DE⊥CE.分析 ①根据直径所对的圆周角是直角,作辅助圆O,可以得到两个点E;
②先证明△ADE∽△BE,列比例式$\frac{AD}{BE}=\frac{AE}{BC}$,设AE=x,BE=8-x,代入得:$\frac{3}{8-x}=\frac{x}{5}$,解得x=5或3;
分两种情况:i)当AE=5,BE=3时,如图2,ii)当AE=5,BE=3时,如图2,利用勾股定理求DE和CE的长,代入面积公式求得结论.
解答 解:①如图所示: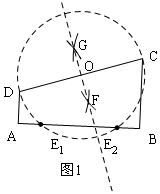
作法:(1)作CD的中垂线FG,交CD于O,
(2)以O为圆心,以OD为半径作圆,交AB于两点:E1、E2,
则E1、E2就是符合条件的点;
②∵AD∥BC,AB⊥BC,
∴AB⊥AD,
∴∠A=∠B=90°,
∴∠AED+∠ADE=90°,
∵DE⊥CE,
∴∠AED+∠BEC=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC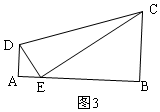 ,
,
∴$\frac{AD}{BE}=\frac{AE}{BC}$,
由已知:AD=3,BC=5,AB=8,则可设AE=x,BE=8-x,
∴$\frac{3}{8-x}=\frac{x}{5}$,
x=5或3,
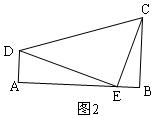
当AE=5,BE=3时,如图2,
DE=CE=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∴S△CDE=$\frac{1}{2}$DE2=$\frac{1}{2}$×$(\sqrt{34})^{2}$=17,
当AE=3,BE=5时,如图3,
DE=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,CE=$\sqrt{{5}^{2}+{5}^{2}}$=5$\sqrt{2}$,
∴S△CDE=$\frac{1}{2}$DE•CE=$\frac{1}{2}$×3$\sqrt{2}$×$5\sqrt{2}$=15,
∴△CED的面积是17或15.
点评 本题考查了直角梯形、直角三角形边和角的关系、勾股定理、三角形相似的性质和判定、圆周角定理以及尺规作图,难度适中,明确直径所对的圆周角是直角,在直角三角形中常利用同角的余角相等证明两个角相等,并采用分类讨论的思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.
如图所示,有一块呈三角形的草坪,其一边长为20m,在这个草坪的图纸上,若这条边的长为5cm,其他两边的长都是3.5cm,则该草坪其他两边的实际长度为14m;14m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
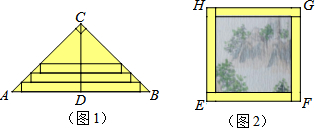
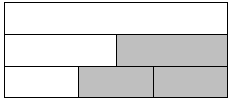 如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )
如图,三个大小相同的长方形拼在一起组成一个大长方形,把第二个长方形平均分成2份;再把第3个长方形平均分成3份,那么图中阴影部分是大长方形面积的( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com