|
|
|
已知反比例函数的图象经过点(－1，2)，则它的解析式是
|
| [ ] |
A． |
|
B． |
|
C． |
|
D． |
|
|
|
练习册系列答案
相关习题
科目：初中数学
来源：人教版（新课标） 八年级（下）
题型：
|
|
|
在比例尺为1∶30000的地图上测得AB两地间的图上距离为8 cm，则两地间的实际距离为________m．
|
|
|
查看答案和解析>>
科目：初中数学
来源：北京课改版 第16册
题型：
|
|
|
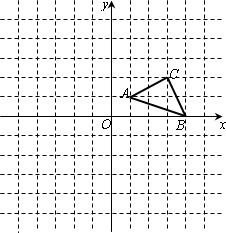
如图所示，直角梯形OABC的直角顶点O是坐标原点，边OA、OC分别在x轴、y轴的正半轴上，OA∥BC，D是BC上一点，4BD＝OA＝4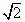 ，AB＝3，∠OAB＝45°，其中点E、F分别是线段OA、AB上的两个动点，且始终保持∠DEF＝45°．
(1)直接写出点D的坐标；
(2)求证：∠OED＝∠AFE；
(3)当△AEF是等腰三角形时，△AEF关于直线EF的对称图形为△ EF，求△ EF与五边形OEFBC的重叠部分的面积．
|
|
|
查看答案和解析>>
科目：初中数学
来源：苏科版（新课标） 九年级上册
题型：
|
|
|
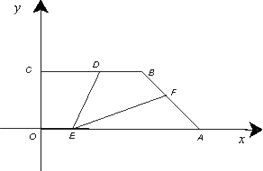
如图，已知O是坐标原点，A、B、C三点的坐标分别为(1，1)、(4，0)、(3，2)．
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1；
(2)画出与△A1B1C1关于原点成中心对称的△A2B2C2，并写出A2、B2、C2三点的坐标．
|
|
|
查看答案和解析>>
科目：初中数学
来源：苏科版（新课标） 九年级上册
题型：
|
|
|
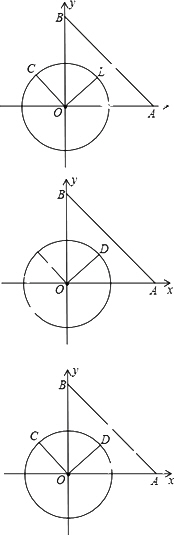
在平面直角坐标系xOy中，已知点A(6，0)，点B(0，6)，动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)，连接AB．
(1)当OC∥AB时，∠BOC的度数为________；
(2)连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．
(3)连接AD，当OC∥AD时，
①求出点C的坐标；
②直线BC是否为⊙O的切线？
请作出判断，并说明理由．
|
|
|
查看答案和解析>>
科目：初中数学
来源：浙教版（新课标） 九年级上册
题型：
|
|
|
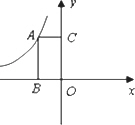
如图，矩形ABOC的面积为3，反比例函数 的图象过点A，则k为
|
| [ ] |
A． |
－3
|
B． |
－1.5
|
C． |
3
|
D． |
－6
|
|
|
查看答案和解析>>
科目：初中数学
来源：浙教版（新课标） 九年级上册
题型：
|
|
|
写出一个开口向下，对称轴是直线x＝2的抛物线解析式________．
|
|
|
查看答案和解析>>
科目：初中数学
来源：浙教版（新课标） 九年级上册
题型：
|
|
|
自然数4、5、5、x、y从小到大排列后，其中位数为4，如果这组数据唯一的众数是5，那么，所有满足条件的x、y中，x＋y的最大值是
|
| [ ] |
A． |
3
|
B． |
4
|
C． |
5
|
D． |
6
|
|
|
查看答案和解析>>
科目：初中数学
来源：浙教版（新课标） 九年级上册
题型：
|
|
|
如图，已知抛物线y＝x2＋bx＋c经过点(1，－5)，(－2，4)
(1)求这条抛物线的解析式．
(2)设该抛物线与直线y＝x相交于点A，B(点B在点A的右侧)，平行于y轴的直线x＝m(0＜m＜ )与抛物线交于点M，与直线y＝x交于点N，交x轴于点P．求线段MN的长(用含m的代数式表示)
(3)在(2)的情况下，连接OM，BM，是否存在m，使△BOM的面积S最大？若存在，求出m的值，若不存在，说明理由．
|
|
|
查看答案和解析>>
