
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】B
【解析】试题分析:由二次函数的图象开口向上可得a>0,根据二次函数的图象与y轴交于正半轴知:c>0,由对称轴直线x=2,可得出b与a异号,即b<0,则abc<0,故①正确;
把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c,由函数图象可以看出当x=﹣1时,二次函数的值为正,即a﹣b+c>0,则b<a+c,故②选项正确;
把x=2代入y=ax2+bx+c得:y=4a+2b+c,由函数图象可以看出当x=2时,二次函数的值为负,即4a+2b+c<0,故③选项错误;
由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2﹣4ac>0,故④D选项正确;
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15). 
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,射线OC⊥OD;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的三角形不一定是直角三角形的是( )
A. 三条边的比为5:12:13
B. 三个角的度数比为2:3:5
C. 有一边等于另一条边的一半
D. 三角形的三边长分别是24、25和7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公园内有一棵大树,为测量树高,小明在D处用测角仪测得树顶端A的仰角为30°,已知测角仪高DC=1.4m,BC=30m,请帮助小明计算出树高AB(![]() 取1.732,结果保留三个有效数字).
取1.732,结果保留三个有效数字).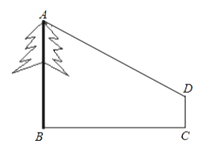
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com