
【题目】袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.
①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
【答案】
(1)解:①画树状图得: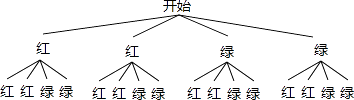
∵共有16种等可能的结果,第一次摸到绿球,第二次摸到红球的有4种情况,
∴第一次摸到绿球,第二次摸到红球的概率为: ![]() .
.
②∵两次摸到的球中有1个绿球和1个红球的有8种情况,
∴两次摸到的球中有1个绿球和1个红球的为: ![]() .
.
(2)![]()
【解析】(1)抓住关键的已知条件:先从袋中摸出1个球后放回,混合均匀后再摸出1个球.列出树状图。先求出所有可能的结果数,①求出第一次摸到绿球,第二次摸到红球的可能数,根据概率公式计算即可;②求出两次摸到的球中有1个绿球和1个红球的可能数,根据概率公式计算即可。
(2)抓住已知条件先从袋中摸出1个球后不放回,再摸出1个球,求出所有可能的结果数及两次摸到的球中有1个绿球和1个红球的可能数,根据概率公式计算即可。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF.你认为( )

A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=![]() +
+![]() -6
-6
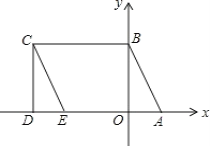
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的大正方形内有一个边长为
的大正方形内有一个边长为![]() 的小正方形.
的小正方形.
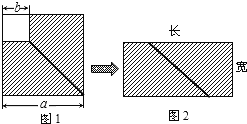
(1)用含字母的代数式表示图1中阴影都分的面积为______________;
(2)图1的阴影部分沿斜线剪开局,拼成了一个如图2所示的长方形,用含字母的代数式表示此长方形的面积为_____________(多项式乘积的形式);
(3)比较左、右两图的阴影都分面积,请你写出一个整式乘法的公式_____________;
(4)结合(3)的公式,计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD,其中AD//BC,AB⊥BC,将DC沿DE折叠,C落于![]() ,
,![]() 交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点
交CB于G,且ABGD为长方形(如图1);再将纸片展开,将AD沿DF折叠,使A点落在DC上一点![]() (如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.
(如图2),在两次折叠过程中,两条折痕DE、DF所成的角为____________度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,对角线
中,对角线![]() 和
和![]() 交于点
交于点![]() ,且点
,且点![]() 是
是![]() 和
和![]() 的中点,若
的中点,若![]() 的长为10,则
的长为10,则![]() 和
和![]() 的长可以是( )
的长可以是( )

A. 5和10B. 8和12C. 10和20D. 20和40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.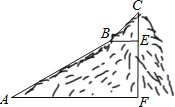
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com