
【题目】已知在Rt△ABC中,∠BAC=90°,AB≥AC,D,E分别为AC,BC边上的点(不包括端点),且![]() =
=![]() =m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
=m,连结AE,过点D作DM⊥AE,垂足为点M,延长DM交AB于点F.
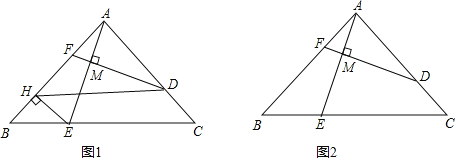
(1)如图1,过点E作EH⊥AB于点H,连结DH.
①求证:四边形DHEC是平行四边形;
②若m=![]() ,求证:AE=DF;
,求证:AE=DF;
(2)如图2,若m=![]() ,求
,求![]() 的值.
的值.
【答案】(1)①证明见解析;②证明见解析;(2)![]()
【解析】(1)①先判断出△BHE∽△BAC,进而判断出HE=DC,即可得出结论;
②先判断出AC=AB,BH=HE,再判断出∠HEA=∠AFD,即可得出结论;
(2)先判断出△EGB∽△CAB,进而求出CD:BE=3:5,再判断出∠AFM=∠AEG进而判断出△FAD∽△EGA,即可得出结论.
(1)①证明:∵EH⊥AB,∠BAC=90°,
∴EH∥CA,
∴△BHE∽△BAC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴HE=DC,
∵EH∥DC,
∴四边形DHEC是平行四边形;
②∵![]() ,∠BAC=90°,
,∠BAC=90°,
∴AC=AB,
∵![]() ,HE=DC,
,HE=DC,
∴HE=DC,
∴![]() ,
,
∵∠BHE=90°,
∴BH=HE,
∵HE=DC,
∴BH=CD,
∴AH=AD,
∵DM⊥AE,EH⊥AB,
∴∠EHA=∠AMF=90°,
∴∠HAE+∠HEA=∠HAE+∠AFM=90°,
∴∠HEA=∠AFD,
∵∠EHA=∠FAD=90°,
∴△HEA≌△AFD,
∴AE=DF;
(2)如图,过点E作EG⊥AB于G,
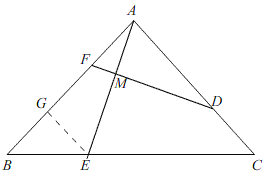
∵CA⊥AB,
∴EG∥CA,
∴△EGB∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴EG=CD,
设EG=CD=3x,AC=3y,
∴BE=5x,BC=5y,
∴BG=4x,AB=4y,
∵∠EGA=∠AMF=90°,
∴∠GEA+∠EAG=∠EAG+∠AFM,
∴∠AFM=∠AEG,
∵∠FAD=∠EGA=90°,
∴△FAD∽△EGA,
∴![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】(1)完成下面的证明(在括号中填写推理理由)如图,已知![]() ,
,![]() ,求证:
,求证:![]() .
.

证明:因为![]() ,
,
所以![]() (________),
(________),
所以![]() ________
________![]() (________).
(________).
因为![]() ,
,
所以![]() ________
________![]() (________).
(________).
所以![]() (________).
(________).
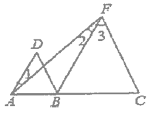
(2)如图,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
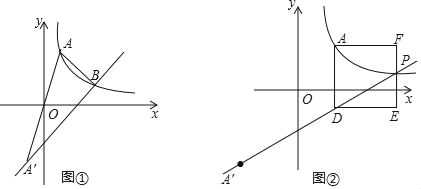
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣2.5表示的点与数 表示的点重合;
(2)若﹣1表示的点与5表示的点重合,回答以下问题:
①5表示的点与数 表示的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
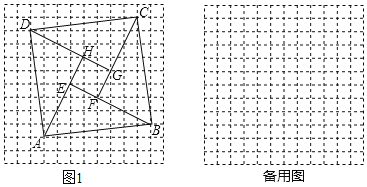
【题目】在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD的边长为![]() ,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为
,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为![]() 时,正方形EFGH的面积的所有可能值是_____(不包括5).
时,正方形EFGH的面积的所有可能值是_____(不包括5).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:
为顺利通过国家义务教育均衡发展验收,我市某中学配备了两个多媒体教室,购买了笔记本电脑和台式电脑共120台,购买笔记本电脑用了7.2万元,购买台式电脑用了24万元,已知笔记本电脑单价是台式电脑单价的1.5倍,那么笔记本电脑和台式电脑的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件不能判定Rt△ABC≌Rt△DEF的是( )
A. AC=DF,∠B=∠EB. ∠A=∠D,∠B=∠E
C. AB=DE,AC=DFD. AB=DE,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设,首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④),这样反复更换地砖的颜色,按照这种规律,直至铺满整个广场,观察下图,解决下列问题.
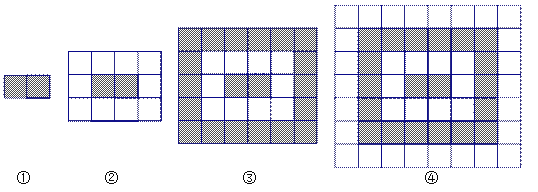
(1)填表
图形序号数 | ① | ② | ③ | ④ | … |
地砖总数(包括黑白地砖) | 2 |
(2)按照这种规律第6个图形一共用去地砖多少块?
(3)按照这种规律第![]() 个图形一共用去地砖多少块?(用含
个图形一共用去地砖多少块?(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com