
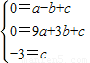 Ј¬
Ј¬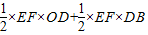 Ј¬
Ј¬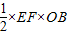 Ј¬
Ј¬ Ј¬
Ј¬ Ј¬
Ј¬ Ј¬
Ј¬ Ј¬SЎчBDEИЎЧоҙуЦө
Ј¬SЎчBDEИЎЧоҙуЦө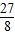 Ј¬өгEөДЧшұкОӘЈЁ
Ј¬өгEөДЧшұкОӘЈЁ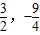 Ј©Ј¬
Ј©Ј¬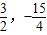 Ј©Ј¬К№ЎчBDEөДГж»эЧоҙуОӘ
Ј©Ј¬К№ЎчBDEөДГж»эЧоҙуОӘ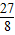 Ј»РЎГчН¬С§ИПОӘЈәЎ°өұEОӘЕЧОпПЯөД¶ҘөгКұЈ¬ЎчBDEөДГж»эЧоҙуЈ®ЎұХвСщөД№ЫөгКЗҙнОуөДЈ®
Ј»РЎГчН¬С§ИПОӘЈәЎ°өұEОӘЕЧОпПЯөД¶ҘөгКұЈ¬ЎчBDEөДГж»эЧоҙуЈ®ЎұХвСщөД№ЫөгКЗҙнОуөДЈ®

 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
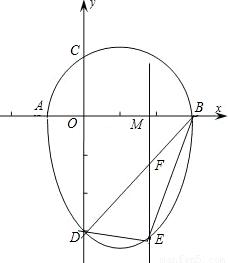
 ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЈ¬өгAЎўBЎўCЎўD·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬өгDөДЧшұкОӘЈЁ0Ј¬-3Ј©ABОӘ°лФІЦұҫ¶Ј¬°лФІФІРДMЈЁ1Ј¬0Ј©Ј¬°лҫ¶ОӘ2Ј¬ФтЎ°ө°ФІЎұөДЕЧОпПЯІҝ·ЦөДҪвОцКҪОӘ
ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЈ¬өгAЎўBЎўCЎўD·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬өгDөДЧшұкОӘЈЁ0Ј¬-3Ј©ABОӘ°лФІЦұҫ¶Ј¬°лФІФІРДMЈЁ1Ј¬0Ј©Ј¬°лҫ¶ОӘ2Ј¬ФтЎ°ө°ФІЎұөДЕЧОпПЯІҝ·ЦөДҪвОцКҪОӘІйҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
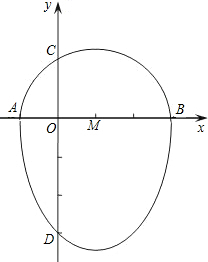 ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЛщКҫЈ¬өгAЎўBЎўCЎўD·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬ТСЦӘөгDөДЧшұкОӘЈЁ0Ј¬-3Ј©Ј¬ABОӘ°лФІөДЦұҫ¶Ј¬°лФІФІРДMөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬°лФІ°лҫ¶ОӘ2Ј®
ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЛщКҫЈ¬өгAЎўBЎўCЎўD·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬ТСЦӘөгDөДЧшұкОӘЈЁ0Ј¬-3Ј©Ј¬ABОӘ°лФІөДЦұҫ¶Ј¬°лФІФІРДMөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬°лФІ°лҫ¶ОӘ2Ј®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
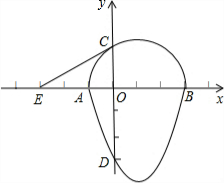 ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЈ¬өгAЈ¬BЈ¬CЈ¬D·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬ТСЦӘөгDөДЧшұкОӘЈЁ0Ј¬-3Ј©Ј¬ABОӘ°лФІөДЦұҫ¶Ј¬°лФІФІРДMөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬°лФІ°лҫ¶ОӘ2Ј¬Фтҫӯ№эөгCөДЎ°ө°ФІЎұЗРПЯECөДҪвОцКҪКЗ
ОТГЗ°СТ»ёц°лФІУлЕЧОпПЯөДТ»Іҝ·ЦәПіЙөД·вұХНјРОіЖОӘЎ°ө°ФІЎұЈ¬Из№ыТ»МхЦұПЯУлЎ°ө°ФІЎұЦ»УРТ»ёцҪ»өгЈ¬ДЗГҙХвМхЦұПЯҪРЧцЎ°ө°ФІЎұөДЗРПЯЈ®ИзНјЈ¬өгAЈ¬BЈ¬CЈ¬D·ЦұрКЗЎ°ө°ФІЎұУлЧшұкЦбөДҪ»өгЈ¬ТСЦӘөгDөДЧшұкОӘЈЁ0Ј¬-3Ј©Ј¬ABОӘ°лФІөДЦұҫ¶Ј¬°лФІФІРДMөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬°лФІ°лҫ¶ОӘ2Ј¬Фтҫӯ№эөгCөДЎ°ө°ФІЎұЗРПЯECөДҪвОцКҪКЗІйҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
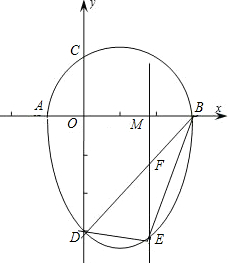 ХэИ·ЈҝМбіцДгөДјыҪвЈ¬ИфЎчBDEөДГж»эҙжФЪЧоҙуЦөЈ¬ЗлЗуіцmөДЦөТФј°өгEөДЧшұкЈ®
ХэИ·ЈҝМбіцДгөДјыҪвЈ¬ИфЎчBDEөДГж»эҙжФЪЧоҙуЦөЈ¬ЗлЗуіцmөДЦөТФј°өгEөДЧшұкЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәФД¶БАнҪв
 ЧРПёФД¶БІўНкіЙПВМвЈә
ЧРПёФД¶БІўНкіЙПВМвЈә| 3 |
| 3 |
| 7 |
| 2 |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com