
 如图,在半径为2的⊙O中,∠AOB=45°,AC是直径,点B在圆上,$\sqrt{2}$≈1.4,则tanC近似值为(精确到0.1)( )
如图,在半径为2的⊙O中,∠AOB=45°,AC是直径,点B在圆上,$\sqrt{2}$≈1.4,则tanC近似值为(精确到0.1)( )| A. | 0.4 | B. | 0.7 | C. | 1.4 | D. | 2.4 |
分析 首先过点A作AD⊥OB于点D,由在Rt△AOD中,∠AOB=45°,可求得AD与OD的长,继而可得BD的长,然后由勾股定理求得AB,BC的长,继而可求得tanC的值.
解答 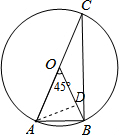 解:过点A作AD⊥OB于点D,
解:过点A作AD⊥OB于点D,
∵在Rt△AOD中,∠AOB=45°,
∴OD=AD=OA•cos45°=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∴BD=OB-OD=2-$\sqrt{2}$,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=2$\sqrt{2-\sqrt{2}}$,
∵AC是⊙O的直径,
∴∠ABC=90°,AC=4,
∴在Rt△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=2$\sqrt{2+\sqrt{2}}$
∴tanC=$\frac{AB}{BC}$≈0.4.
故选:A.
点评 此题考查了圆周角定理、三角函数以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A、C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E、F,则四边形EMFD面积的最大值为( )
如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A、C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E、F,则四边形EMFD面积的最大值为( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
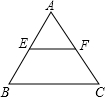 如图所示,刘伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是25 米.
如图所示,刘伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是25 米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一副三角板按如图(4)所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的边CD与△AOB的某一边平行时,相应的旋转角α的值是30°,75°,165°.
一副三角板按如图(4)所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的边CD与△AOB的某一边平行时,相应的旋转角α的值是30°,75°,165°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
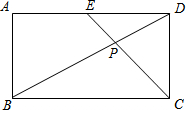 学完第七章《平面直角坐标系》和第十九章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=4,AB=2,点E为AD的中点,BD和CE相交于点P.求△BPC的面积.
学完第七章《平面直角坐标系》和第十九章《一次函数》后,老师布置了这样一道思考题:已知:如图,在长方形ABCD中,BC=4,AB=2,点E为AD的中点,BD和CE相交于点P.求△BPC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com