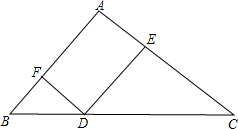
(1)解:∵DF∥AC,DE∥AB,
∴∠B=∠CDE,∠BFD=∠A,
∴△BDF∽△DCE,
∴S
△BDF:S
△DCE=BD
2:DC
2=4:9,
∴BD:DC=2:3,
∴BD:BC=2:5,
又∵DF∥AC,
∴△BFD∽△BAC,
∴S
△BFD:S
△BAC=BD
2:BC
2=4:25,
∴S
△ABC=25.
(2)证明:设BD=a,DC=b,
∵△BFD∽△BAC,
∴
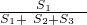
=
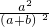
①,
∵△CED∽△CAB,
∴
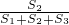
=
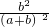
②,
①+②得,
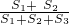
=
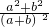
,
∴
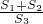
=
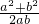
,
由(a-b)
2≥0,即a
2+b
2≥2ab,
∴S
1+S
2≥S
3,
当a
2+b
2=2ab,即(a-b)
2=0,S
1+S
2=S
3成立.
∴a=b,即点D是BC的中点.
分析:(1)由DF∥AC,DE∥AB,得△BDF∽△DCE,根据相似三角形的性质得S
△BDF:S
△DCE=BD
2:DC
2=4:9,则BD:DC=2:3,得到
BD:BC=2:5,又△BFD∽△BAC,得到S
△BFD:S
△BAC=BD
2:BC
2=4:25,即可得到△ABC的面积.
(2)设BD=a,DC=b,由△BFD∽△BAC,得
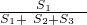
=
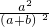
①;由△CED∽△CAB,得
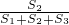
=
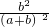
②,
①+②得,
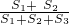
=
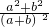
,利用比例的性质得
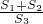
=
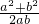
≥1,即可得到结论.当(a-b)
2=0,S
1+S
2=S
3成立,即点D是BC的中点.
点评:本题考查了三角形相似的判定与性质:平行于三角形一边的直线截其它两边,截得的三角形与原三角形相似;相似三角形面积的比等于相似比的平方.也考查了比例和不等式的性质.

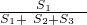 =
=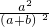 ①,
①,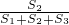 =
=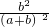 ②,
②,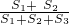 =
=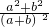 ,
,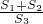 =
=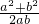 ,
,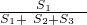 =
=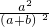 ①;由△CED∽△CAB,得
①;由△CED∽△CAB,得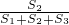 =
=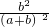 ②,
②,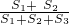 =
=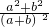 ,利用比例的性质得
,利用比例的性质得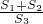 =
=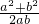 ≥1,即可得到结论.当(a-b)2=0,S1+S2=S3成立,即点D是BC的中点.
≥1,即可得到结论.当(a-b)2=0,S1+S2=S3成立,即点D是BC的中点.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为