Question

【题目】如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．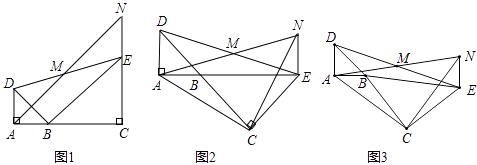

（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；
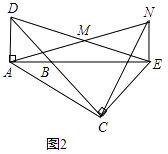
（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；
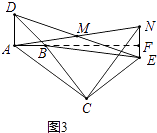
（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

Answer 1

【答案】
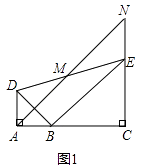
（1）证明：如图1，

∵EN∥AD，

∴∠MAD=∠MNE，∠ADM=∠NEM．

∵点M为DE的中点，

∴DM=EM．

在△ADM和△NEM中，

∴ ．

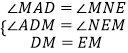∴△ADM≌△NEM．

∴AM=MN．

∴M为AN的中点

（2）证明：如图2，

∵△BAD和△BCE均为等腰直角三角形，

∴AB=AD，CB=CE，∠CBE=∠CEB=45°．

∵AD∥NE，

∴∠DAE+∠NEA=180°．

∵∠DAE=90°，

∴∠NEA=90°．

∴∠NEC=135°．

∵A，B，E三点在同一直线上，

∴∠ABC=180°﹣∠CBE=135°．

∴∠ABC=∠NEC．

∵△ADM≌△NEM（已证），

∴AD=NE．

∵AD=AB，

∴AB=NE．

在△ABC和△NEC中，

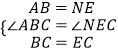
∴△ABC≌△NEC．

∴AC=NC，∠ACB=∠NCE．

∴∠ACN=∠BCE=90°．

∴△ACN为等腰直角三角形

（3）证明：△ACN仍为等腰直角三角形．

证明：如图3，延长AB交NE于点F，

∵AD∥NE，M为中点，

∴易得△ADM≌△NEM，

∴AD=NE．

∵AD=AB，

∴AB=NE．

∵AD∥NE，

∴AF⊥NE，

在四边形BCEF中，

∵∠BCE=∠BFE=90°

∴∠FBC+∠FEC=360°﹣180°=180°

∵∠FBC+∠ABC=180°

∴∠ABC=∠FEC

在△ABC和△NEC中，

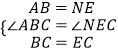
∴△ABC≌△NEC．

∴AC=NC，∠ACB=∠NCE．

∴∠ACN=∠BCE=90°．

∴△ACN为等腰直角三角形．

【解析】（1）由EN∥AD和点M为DE的中点可以证到△ADM≌△NEM，从而证到M为AN的中点．（2）易证AB=DA=NE，∠ABC=∠NEC=135°，从而可以证到△ABC≌△NEC，进而可以证到AC=NC，∠ACN=∠BCE=90°，则有△ACN为等腰直角三角形．（3）延长AB交NE于点F，易得△ADM≌△NEM，根据四边形BCEF内角和，可得∠ABC=∠FEC，从而可以证到△ABC≌△NEC，进而可以证到AC=NC，∠ACN=∠BCE=90°，则有△ACN为等腰直角三角形．