
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
分析 设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为$\frac{15-2x}{3}$个,分0≤x<3和3≤x两种情况考虑,分别找出y关于x的函数关系式,再利用一次函数的性质即可解答.
解答 解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为$\frac{15-2x}{3}$个,
①当0≤x<3时,y=5x+$\frac{15-2x}{3}$×6=x+30,
∵k=1>0,
∴y随x的增大而增大,
∴当x=0时,y有最小值,最小值为30元;
②当3≤x时,y=5x+$\frac{15-2x}{3}$×6-4=26+x,
∵k=1>0,
∴y随x的增大而增大,
∴当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.
故答案为:29.
点评 本题考查了列代数式以及一次函数的性质,分别0≤x<3和3≤x两种情况找出y关于x的函数关系式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
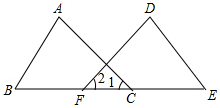 在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
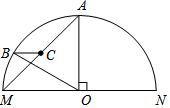 如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.
如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com