
 如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:044
“青朱出入图”真是“无字的证明”.如图所示也是一种“无字证明”方法.做法是:过较大正方形的中心,作两条互相垂直的线,将其分成4份.然后,将这四个部分围在四周,小正方形填在中间,恰好得到大正方形.当然,“两条互相垂直的线”可有很多,你如何选择一条恰当的呢?亲自做一做,你可能会有更多的收获!

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
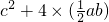 ,即
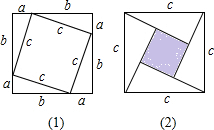
,即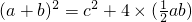 ,由此推导出一个重要的结论:a2+b2=c2,这个重要的结论就是著名的“勾股定理”.请你用两种方法求图(2)的大正方形面积,并验证勾股定理(其中四个直角三角形的较小的直角边长都为a,较大的直角边长都为b,斜边长都为c).
,由此推导出一个重要的结论:a2+b2=c2,这个重要的结论就是著名的“勾股定理”.请你用两种方法求图(2)的大正方形面积,并验证勾股定理(其中四个直角三角形的较小的直角边长都为a,较大的直角边长都为b,斜边长都为c).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com