
分析 (1)根据题意可以求得$\sqrt{2{x}^{2}+2}$的值;
(2)根据x是正数,$\sqrt{2{x}^{2}+2}$是整数,可以求得x的最小值;
(3)根据$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式,且被开方数相同,可以求得x的值.
解答 解:(1)当x=3时,
$\sqrt{2{x}^{2}+2}$=$\sqrt{2×{3}^{2}+2}=\sqrt{20}=2\sqrt{5}$;
(2)∵x是正数,$\sqrt{2{x}^{2}+2}$是整数,
∴$\sqrt{2{x}^{2}+2}$的最小值是2,
解得,x=1或x=-1(舍去),
即x的最小值是1;
(3)∵$\sqrt{2{x}^{2}+2}$和$\sqrt{2{x}^{2}+x+4}$是两个最简二次根式,且被开方数相同,
∴2x2+2=2x2+x+4,
解得,x=-2,
即x的值是-2.
点评 本题考查同类二次根式,解题的关键是明确题意,找出所求问题需要的条件.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
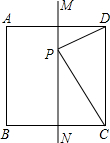 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点当PC+PD最小时,∠PCD=( )°.| A. | 60° | B. | 45° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
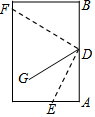 小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )
小明同学把一张长方形纸折了两次,如图,使点A、B都落在DG上,折痕分别是DE、DF,则∠EDF的度数为( )| A. | 60° | B. | 75° | C. | 90° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com