练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，

    ①写出A、B、C的坐标．

    ②以原点O为对称中心，画出△ABC关于原点O对称的△A1B1C1，并写出A1、B1、C1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016届山东聊城中考数学预测试卷（二）数学试卷（解析版） 题型：填空题

    已知关于x的方程3a+x=﹣5的解为2，a的值是 ．

    查看答案和解析>>

    科目：初中数学 来源：2017届江西崇仁县二中九年级上期中考试数学试卷（解析版） 题型：解答题

    2013年，江阴市某楼盘以每平方米6500元的均价对外销售，因为楼盘滞销，房地产开发商为了加快资金周转，决定进行降价促销，经过连续两年下调后，2015年的均价为每平方米5265元．

    （1）求平均每年下调的百分率；

    （2）假设2016年的均价仍然下调相同的百分率，张强准备购买一套100平方米的住房，他持有现金20万元，可以在银行贷款30万元，张强的愿望能否实现？（房价每平方米按照均价计算）

    查看答案和解析>>

    科目：初中数学 来源：2017届江西崇仁县二中九年级上期中考试数学试卷（解析版） 题型：选择题

    下列说法正确的是( )

    A、平分弦的直径垂直于弦

    B、三角形的外心到这个三角形的三边距离相等

    C、相等的圆心角所对的弧相等

    D、等弧所对的圆心角相等

    查看答案和解析>>

    科目：初中数学 来源：2017届辽宁营口大石桥市九年级上期中数学卷（解析版） 题型：解答题

    如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，联结AD，以AD为一边且在AD的右侧作正方形ADEF．

    （1）如果AB=AC，∠BAC=90°，

    ①当点D在线段BC上时（与点B不重合），如图2，将△ABD绕A点逆时针旋转90°，所得到的三角形为 ，线段CF、BD所在直线的位置关系为 ，线段CF、BD的数量关系为 ；

    ②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；

    （2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2017届辽宁营口大石桥市九年级上期中数学卷（解析版） 题型：填空题

    若实数a、b满足（4a+4b）（4a+4b﹣2）﹣8=0，则a+b= ．

    查看答案和解析>>

    科目：初中数学 来源：2017届辽宁营口大石桥市九年级上期中数学卷（解析版） 题型：选择题

    已知点A（a，2015）与点A′（﹣2016，b）是关于原点O的对称点，则a+b的值为（ ）.

    A．1 B．5 C．6 D．4

    查看答案和解析>>

    科目：初中数学 来源：2017届山东东营利津县九年级秋季学业水平考试期中数学卷（解析版） 题型：填空题

    某生物兴趣小组的学生将自己收集的标本向本组其他成员各赠送一件，全组共互赠了182件，如果全组有x名同学，那么根据题意列出的方程是___________ .

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年山东威海环翠区七年级五四制上期中考试数学卷（解析版） 题型：解答题

    问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？

    问题探究：不妨假设能搭成种不同的等腰三角形，为探究之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．

    探究一：

    （1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    此时，显然能搭成一种等腰三角形。所以，当时，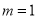

    （2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形

    所以，当时，

    （3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形

    若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形

    所以，当时，

    （4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？

    若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形

    若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形

    所以，当时，

    综上所述，可得表①

    3

    4]

    5

    6

    1

    0

    1

    1

    探究二：

    （1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？

    （仿照上述探究方法，写出解答过程，并把结果填在表②中）

    （2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三

    角形？（只需把结果填在表②中）

    7

    8

    9

    10

    你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……

    解决问题：用根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？

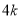    （设分别等于、、、，其中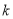是整数，把结果填在表③中）

    问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）

    查看答案和解析>>

    同步练习册答案