
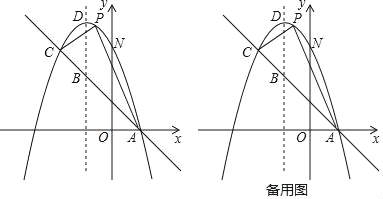
����Ŀ����ͼ����֪������y����x2+bx+c��һֱ���ཻ��A��1��0����C����2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1����������ֱ��AC�ĺ�����ϵʽ��
��2����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ����ʱ��P�����ꣻ
��3���ڶԳ������Ƿ����һ��M��ʹ��ANM���ܳ���С�������ڣ������M����������ANM�ܳ�����Сֵ���������ڣ���˵�����ɣ�
���𰸡���1��y����x2��2x+3��y����x+1����2����x����![]() ʱ����APC�����ȡ���ֵ�����ֵΪ
ʱ����APC�����ȡ���ֵ�����ֵΪ![]() ����ʱ��P������Ϊ����
����ʱ��P������Ϊ����![]() ��
��![]() ������3���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM���ܳ���С����ANM�ܳ�����СֵΪ3
������3���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM���ܳ���С����ANM�ܳ�����СֵΪ3![]() ��
��
��������
��1�����ݵ�A��C�����꣬���ô���ϵ�����������������ֱ��AC�ĺ�����ϵʽ����2������P��PE��y�ύx���ڵ�E����ֱ��AC�ڵ�F������C��CQ��y�ύx���ڵ�Q�����P������Ϊ��x����x2��2x+3������2��x��1�������E������Ϊ��x��0������F������Ϊ��x����x+1���������ɵó�PF��ֵ���ɵ�C������ɵó���Q�����꣬�����ɵó�AQ��ֵ�����������ε������ʽ�ɵó�S��APC����![]() x2��
x2��![]() x+3�������ö��κ��������ʣ����ɽ����ֵ���⣻��3�����ö��κ���ͼ���ϵ�����������ɵó���N�����꣬�����䷽�����ҳ������ߵĶԳ��ᣬ�ɵ�C��N������ɵó���C��N���������ߵĶԳ���Գƣ���ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M�����ʱ��ANM�ܳ�ȡ��Сֵ��������һ�κ���ͼ���ϵ���������������M�����꣬�Լ����������ľ��빫ʽ��������ε��ܳ���ʽ�����ANM�ܳ�����Сֵ���ɵó����ۣ�
x+3�������ö��κ��������ʣ����ɽ����ֵ���⣻��3�����ö��κ���ͼ���ϵ�����������ɵó���N�����꣬�����䷽�����ҳ������ߵĶԳ��ᣬ�ɵ�C��N������ɵó���C��N���������ߵĶԳ���Գƣ���ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M�����ʱ��ANM�ܳ�ȡ��Сֵ��������һ�κ���ͼ���ϵ���������������M�����꣬�Լ����������ľ��빫ʽ��������ε��ܳ���ʽ�����ANM�ܳ�����Сֵ���ɵó����ۣ�
��1����A��1��0����C����2��3������y����x2+bx+c���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵĺ�����ϵʽΪy����x2��2x+3��
��ֱ��AC�ĺ�����ϵʽΪy��mx+n��m��0����
��A��1��0����C����2��3������y��mx+n���ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy����x+1��
��2������P��PE��y�ύx���ڵ�E����ֱ��AC�ڵ�F������C��CQ��y�ύx���ڵ�Q����ͼ1��ʾ��
���P��������x����x2��2x+3������2��x��1�������E��������x��0������F��������x����x+1����
��PE����x2��2x+3��EF����x+1��EF��PE��EF����x2��2x+3������x+1������x2��x+2��
����C����������2��3����
����Q����������2��0����
��AQ��1������2����3��
��S��APC��![]() AQPF����
AQPF����![]() x2��
x2��![]() x+3����
x+3����![]() ��x+
��x+![]() ��2+
��2+![]() ��
��
����![]() ��0��
��0��
����x����![]() ʱ����APC�����ȡ���ֵ�����ֵΪ
ʱ����APC�����ȡ���ֵ�����ֵΪ![]() ����ʱ��P������Ϊ����
����ʱ��P������Ϊ����![]() ��
��![]() ����
����
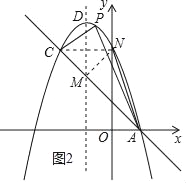
��3����x��0ʱ��y����x2��2x+3��3��
����N��������0��3����
��y����x2��2x+3������x+1��2+4��
�������ߵĶԳ���Ϊֱ��x����1��
����C����������2��3����
����C��N���������ߵĶԳ���Գƣ�
��ֱ��AC�������ߵĶԳ���Ľ���Ϊ��M����ͼ2��ʾ��
����C��N���������ߵĶԳ���Գƣ�
��MN��CM��
��AM+MN��AM+MC��AC��
����ʱ��ANM�ܳ�ȡ��Сֵ��
��x����1ʱ��y����x+1��2��
����ʱ��M������Ϊ����1��2����
����A��������1��0������C����������2��3������N��������0��3����
��AC��![]() ��3
��3![]() ��AN��
��AN��![]() ��
��![]() ��
��
��C��ANM��AM+MN+AN��AC+AN��3![]()
![]() ��
��
���ڶԳ����ϴ���һ��M����1��2����ʹ��ANM���ܳ���С����ANM�ܳ�����СֵΪ3![]() +
+![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
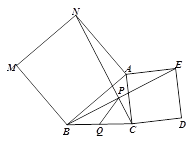
����Ŀ��̽������ͼ���ֱ��ԡ�ABC������AB��ACΪ��������������ABMN��������ACDE��CN��BE���ڵ�P. ��֤����ANC = ��ABE.
Ӧ�ã�Q���߶�BC���е㣬����PQ. ��BC = 6����PQ = ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ������������y= ![]() ��ͼ����һ�κ���y=x+b��ͼ��
��ͼ����һ�κ���y=x+b��ͼ��
�ڵ�A��1��4������B��-4��n����

��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����OAB�������
��3��ֱ��д��һ�κ���ֵ���ڷ���������ֵ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧϰ�����������������磬���������һ��ʱ����a�ǿ�b�ķ������������亯����ϵʽ����дΪ![]() ��sΪ������s��0����
��s������s��0����
���������������һ�����ճ����������ѧϰ�о��з�����������ϵ������ʵ������д�����ĺ�����ϵʽ��
ʵ���������ε����Sһ��ʱ�������εױ߳�y�Ǹ�x�ķ�����������
������ϵʽ���� ����sΪ������s��0����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y��![]() (k��0��k�dz���)��ͼ�����P(��3,5)��
(k��0��k�dz���)��ͼ�����P(��3,5)��
(1)��˷����������Ľ���ʽ��
(2)�ں���ͼ����������(a1��b1)��(a2��b2)����a1��a2�����ж�b1��b2�Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
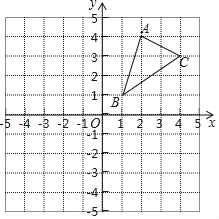
����Ŀ����1���뻭����ABC����x��ԳƵġ�A1B1C1����д����A1�����꣮
��2���뻭����ABC�Ƶ�B��ʱ����ת90���ġ�A2BC2��
��3�������2����C����ת��C2����������·����������������źͦУ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ���.
��1����A��B��C�����ꣻ
��2����MΪ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N.����P�ڵ�Q��ߣ�������PQMN���ܳ����ʱ������AEM�������
��3���ڣ�2���������£�������PMNQ���ܳ����ʱ������DQ.����������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ���.��FG=![]() DQ�����F������.
DQ�����F������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
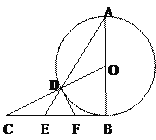
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����BC�ǡ�O�����ߣ�OC���O�ཻ�ڵ�D������AD���ӳ�����BC�ཻ�ڵ�E��
��1����BC��![]() ��CD��1�����O�İ뾶��
��CD��1�����O�İ뾶��
��2��ȡBE���е�F������DF����֤��DF�ǡ�O�����ߡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
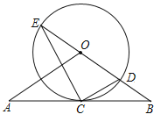
����Ŀ����֪����ͼ���ڡ�OAB�У�OA=OB����O����AB���е�C����OB���ڵ�D������BO���ӳ��߽��ڵ�E������EC��CD��
��1�����ж�AB����O��λ�ù�ϵ��������֤����
��2����tanE=![]() ����O�İ뾶Ϊ3����OA�ij���
����O�İ뾶Ϊ3����OA�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com