
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
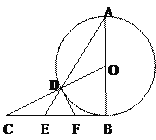
【答案】(1)解:∵AB是⊙O的直径,BC是⊙O的切线∴AB⊥BC,
设⊙O的半径为![]() ,在Rt△OBC中,∵
,在Rt△OBC中,∵![]()
∴![]() ,解得
,解得![]() =1,∴⊙O的半径为1
=1,∴⊙O的半径为1
(2)连结OF,∵OA=OB,BF=EF,∴OF∥AE,∠A=∠2
又∵∠BOD=2∠A,∴∠1=∠2,
又∵OB=OD、OF=OF∴△OBF≌△ODF,
∴∠ODF=∠OBF=900,即OD⊥DF,∴FD是⊙O的切线。
【解析】(1)先设⊙O的半径为r,由于AB是⊙O的直径,BC是⊙O的切线,根据切线性质可知AB⊥BC,在Rt△OBC中,利用勾股定理可得![]() ,解得r=1;
,解得r=1;
(2)连接OF,由于OA=OB,BF=EF,可知OF是△BAE的中位线,那么OF∥AE,于是∠A=∠2,根据三角形外角性质可得∠BOD=2∠A,易证∠1=∠2,而OD=OB,OF=OF,利用SAS可证△OBF≌△ODF,那么∠ODF=∠OBF=90°,于是OD⊥DF,从而可证FD是⊙O的切线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,△ABC的三个顶点及D、E、F、G、H、五个点分别位于小正方形的顶点上. 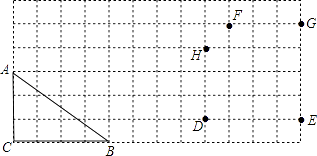
(1)画出△ABC绕点B顺时针方向旋转90°后的图形.
(2)先从E、F、G、H四个点中任意取两个不同的点,再和D点构成三角形,求所得三角形与△ABC面积相等的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校“阅读工程”的开展情况.市教育局从该校初中生中随机抽取了150名学生进行了阅读情况的问卷调查,绘制了如下不完全的统计图: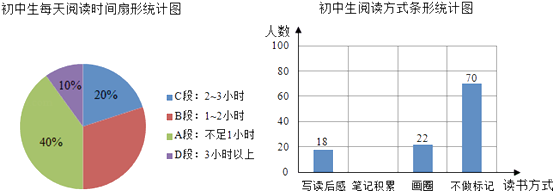
根据上述统计图提供的信息,解答下列问题:
(1)每天阅读时间在1﹣2小时学生有多少人?
(2)采用“笔记积累”阅读方式的学生有多少人?
(3)补全条形统计图.
(4)若将写读后感、笔记积累、画圈点读三种方式称为记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数阵是由偶数排列而成的: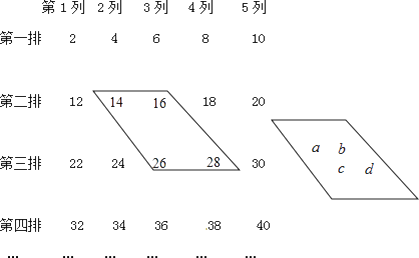
(1)在数阵中任意作一类似的框,如果这四个数的和为188,能否求出这四个数?如果能,求出这些数,如果不能,说明理由.如果和为288,能否求出这四个数?说明理由.
(2)有理数110在上面数阵中的第排、第列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有16个球,其中红球6个,白球和黑球个若干个,每个球除了颜色外没有任何区别.
(1)小明通过大量反复的试验(每次将球搅匀后,任意摸出一个球记下颜色后再放回)发现,取出黑球的频率稳定在 ![]() 附近,请你估计袋中白球的个数;
附近,请你估计袋中白球的个数;
(2)若小明取出的第一个球是白色,将它放在桌上,闭上眼睛从袋中余下的球中再任意取出一个球,取出红球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方米的廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
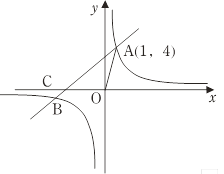
【题目】如图所示,直线AB与反比例函数![]() 的图像相交于A,B两点,已知A(1,4).
的图像相交于A,B两点,已知A(1,4).
(1)求反比例函数的解析式;
(2)直线AB交![]() 轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.
轴于点C,连结OA,当△AOC的面积为6时,求直线AB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com