
【题目】二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )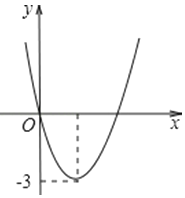
A.-3
B.3
C.-6
D.9
【答案】B
【解析】解:(法1)∵抛物线的开口向上,顶点纵坐标为﹣3,
∴a>0, 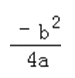 =﹣3,即b2=12a,
=﹣3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2﹣4am≥0,即12a﹣4am≥0,即12﹣4m≥0,解得m≤3,
∴m的最大值为3.
(法2)一元二次方程ax2+bx+m=0有实数根,
可以理解为y=ax2+bx和y=﹣m有交点,
可见﹣m≥﹣3,
∴m≤3,
∴m的最大值为3.
故选B.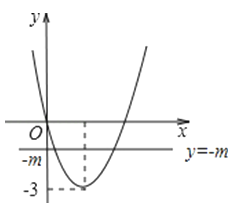
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: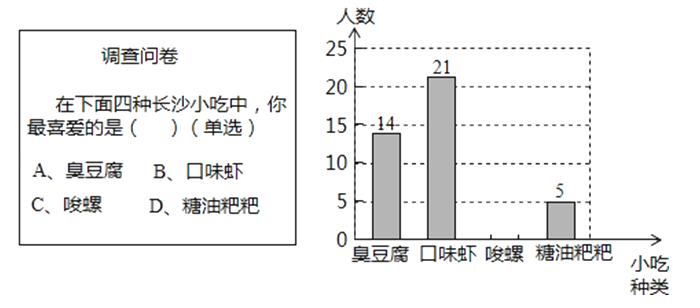
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨.梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=3m.
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度.(结果保留根号)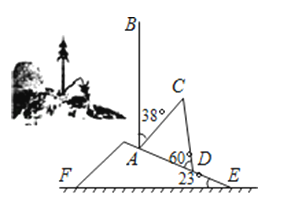
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(![]() ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A,B,C分别表示有理数a,b,c,
(1)当n=1时,
①点A,B,C三点在数轴上的位置如图所示,a,b,c三个数的乘积为正数,数轴上原点的位置可
A.在点A左侧或在A,B两点之间 B.在点C右侧或在A,B两点之间
C.在点A左侧或在B,C两点之间 D.在点C右侧或在B,C两点之间
②若这三个数的和与其中的一个数相等,求a的值;
(2)将点C向右移动(n+2)个单位得到点D,点D表示有理数d,a、b、c、d四个数的积为正数,这四个数的和与其中的两个数的和相等,且a为整数,请在数轴上标出点D并用含n的代数式表示a.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com