
 如图,半径为2
如图,半径为2 的⊙O内有互相垂直的两条弦AB、CD相交于P点.
的⊙O内有互相垂直的两条弦AB、CD相交于P点.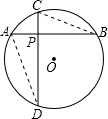 解:(1)连接AD,BC,
解:(1)连接AD,BC,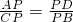 ,
, )2-42=4,ON2=(2
)2-42=4,ON2=(2 )2-32=11,
)2-32=11,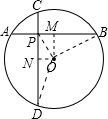
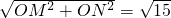 .
. )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个. 

 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com