Question

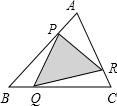
如图所示，△ABC中，点P在边AB上，AP=AB，Q点在边BC上，BQ=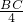，R点在CA边上，CR=CA，已知阴影△PQR的面积是19平方厘米，那么△ABC的面积是________平方厘米．

Answer 1

45.6
分析：利用三角形的面积与边长之间的关系，求出阴影部分面积与三角形ABC的关系，代入阴影部分的面积即可求出△ABC的面积．
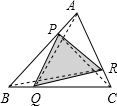解答：解：如图所示，连接AQ，则有△ABQ．
∵BQ=BC，
∴S_△ABQ=S_△ABC，又AP=AB，
∴S_△PBQ=S_△ABQ=×S_△ABC=S_△ABC．
连接BR，
∵RC=AC，
∴S_△BCR=S_△ABC，
又∵BQ=BC，
∴S_△QCR=S_△BCR=S_△ABC．
连接CP，
∵AP=AB，
∴S_△ACP=S_△ABC，
又∵RC=AC，
∴S_△APR=S_△ACP=S_△ABC．
即：S_△PBQ+S_△QCR+S_△APR=（++）S_△ABC=S_△ABC，
S_阴影△PQR=（1-）S_△ABC=S_△ABC=19，
∴S_△ABC=×19=45.6（平方厘米）．
故答案为45.6．
点评：本题主要考查了三角形面积公式的灵活应用，关键在于找出阴影部分的面积与△ABC的面积之间的关系．