
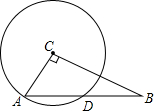
 如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.分析 (1)在Rt△ACB中利用∠B的正弦可计算出AC的长;
(2)作CH⊥AD于H,如图,则根据垂径定理得到AH=DH,再根据等角的余角相等得到∠B=∠ACH,则在Rt△ACH中,利用∠ACH的正弦可计算出AH,从而得到AD的长.
解答 解:(1)在Rt△ACB中,∵sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴AC=$\frac{3}{5}$×10=6,
即⊙C的半径r=6;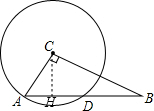 (2)作CH⊥AD于H,如图,则AH=DH,
(2)作CH⊥AD于H,如图,则AH=DH,
∵∠A+∠B=90°,∠A+∠ACH=90°,
∴∠B=∠ACH,
在Rt△ACH中,∵sin∠ACH=$\frac{AH}{AC}$=$\frac{3}{5}$,
∴AH=$\frac{3}{5}$×6=$\frac{18}{5}$,
∴AD=2AH=$\frac{36}{5}$.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了解直角三角形.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
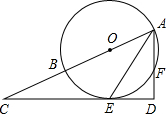 如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
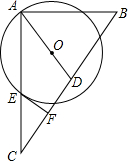 如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
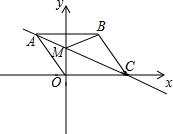 已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标
已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标查看答案和解析>>
科目:初中数学 来源: 题型:解答题
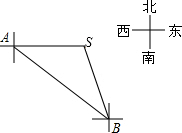 为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)
为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com