
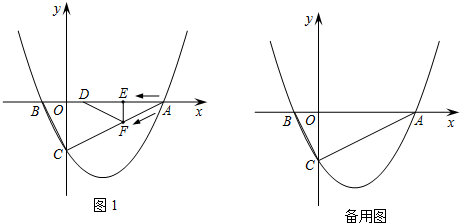
���� ��1������������ͼ����A�Լ�����x=-2��x=5ʱ���κ����ĺ���ֵy��ȡ������������г��������������ϵ����ֵ��
��2���������������߽���ʽ�ܵõ���A��B��C��������꣬���߶�OA��OB��OC�ij�����һ���ܵó�AB��BC��AC�ij���������t ��ʾ���߶�AD��AE��AF����DF���ij��������AE��EF��OA��OC�ij��Լ������ǡ�OAC���ж���AEF����AOC���ƣ���ô��AEFҲ��һ��ֱ�������Σ�����AEF��ֱ�ǣ�����DCF��ֱ�ǣ��ɷֳ�����������ۣ�
i������CΪֱ�Ƕ��㣬���ڡ�ABCǡ����ֱ�������Σ����Ե�CΪֱ�Ƕ��㣬���Դ�ʱ��B��D�غϣ��ɴ˵õ�AD�ij����������t��ֵ��
ii������DΪֱ�Ƕ��㣬��ʱ��CDB���CBDǡ���ǵȽǵ���ǣ��ɴ˿�֤��OB=OD���ٵõ�AD�ij�������t��ֵ��
iii������FΪֱ�Ƕ��㣬����F���߶�AC��ʱ����DFC����ǣ�����F������AC���ӳ�����ʱ����DFC���Ƕ۽ǣ���������������������⣮
�ڴ�����Ҫ������������ۣ�
i��������E�ڵ�A���߶�AB�е�֮��ʱ�����������ε��ص�������������DEF��
ii��������E���߶�AB�е����O֮��ʱ���ص������Ǹ��������ı��Σ���ô��������ɴ�ֱ����������С�۽������ε��������ã�
iii��������E���߶�OB��ʱ���ص������Ǹ�Сֱ�������Σ�
���  �⣺��1���������$\left\{\begin{array}{l}{16a+4b-2=0}\\{4a-2b-2=25a+5b-2}\end{array}\right.$
�⣺��1���������$\left\{\begin{array}{l}{16a+4b-2=0}\\{4a-2b-2=25a+5b-2}\end{array}\right.$
��ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$��
��2�����ɣ�1��֪���κ���Ϊy=$\frac{1}{2}$x2-$\frac{3}{2}$x-2
��A��4��0����
��B��-1��0����C��0��-2��
��OA=4��OB=1��OC=2
��AB=5��AC=2$\sqrt{5}$��BC=$\sqrt{5}$
��AC2+BC2=25=AB2
���ABCΪֱ�������Σ��ҡ�ACB=90��
��AE=2t��AF=$\sqrt{5}$t��
��$\frac{AF}{AE}$=$\frac{AB}{AC}$=$\frac{\sqrt{5}}{2}$
�֡ߡ�EAF=��CAB��
���AEF�ס�ACB
���AEF=��ACB=90��
���AEF��EF���ۺ�A����x���ϵ�D����
�ɷ���֪��DE=AE��
��AD=2AE=4t��EF=$\frac{1}{2}$AE=t
�����DCFΪֱ��������
����F���߶�AC��ʱ
������CΪֱ�Ƕ��㣬���D���B�غϣ���ͼ2
��AE=$\frac{1}{2}$AB=$\frac{5}{2}$t=$\frac{5}{2}$��2=$\frac{5}{4}$��
������DΪֱ�Ƕ��㣬��ͼ3
�ߡ�CDF=90�㣬
���ODC+��EDF=90��
�ߡ�EDF=��EAF��
���OBC+��EAF=90��
���ODC=��OBC��
��BC=DC
��OC��BD��
��OD=OB=1
��AD=3��
��AE=$\frac{3}{2}$
��t=$\frac{3}{4}$��
����F��AC�ӳ�����ʱ����DFC��90�㣬��DCFΪ�۽�������
��������������ʱ��t��ʹ�á�DCFΪֱ�������Σ�t=$\frac{3}{4}$��t=$\frac{5}{4}$��
�ڢ�����0��t��$\frac{5}{4}$ʱ���ص�����Ϊ��DEF����ͼ1��ͼ2
��S=$\frac{1}{2}$��2t��t=t2��
������$\frac{5}{4}$��t��2ʱ����DF��BC�ཻ�ڵ�G�����ص�����Ϊ�ı���BEFG����ͼ4
����G��GH��BE��H����GH=m
��BH=$\frac{m}{2}$��DH=2m����DB=$\frac{3m}{2}$
��DB=AD-AB=4t-5
��$\frac{3m}{2}$=4t-5��
��m=$\frac{2}{3}$��4t-5��
��S=S��DEF-S��DBG=$\frac{1}{2}$��2t��t-$\frac{1}{2}$��4t-5����$\frac{2}{3}$��4t-5��=-$\frac{13}{3}$t2+$\frac{40}{3}$t-$\frac{25}{3}$��
������2��t��$\frac{5}{2}$ʱ���ص�����Ϊ��BEG����ͼ5
��BE=DE-DB=2t-��4t-5��=5-2t��GE=2BE=2��5-2t��
��S=$\frac{1}{2}$����5-2t����2��5-2t��=4t2-20t+25��
���� ������Ҫ������Ƕ��㺯�����⣬�漰�˺�������ʽ��ȷ����ֱ���������Լ����������ε��ж������ʡ����������ε������Լ�ͼ������Ľⷨ���ۺ�֪ʶ���ڶ��������С���漰������϶࣬һ��Ҫ���ݶ���IJ�ͬλ�����������ۣ�ץס����Ĺؼ�λ����ȷ��δ֪����ȡֵ��Χ�ǽ���Ĺؼ����ڣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ͬһ��ֱ���ϵ�������ȷ��һ��Բ | |
| B�� | ��ȵ�Բ�Ľ����ԵĻ���� | |
| C�� | ƽ���ҵ�ֱ����ֱ���� | |
| D�� | ��ͬԲ���Բ�У���ȵ������Ե�Բ�ܽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
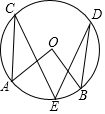 ��ͼ����A��B��C��D��E�ڡ�O�ϣ�����ACE=25�㣬��BDE=15�㣬��Բ�Ľǡ�AOB�Ĵ�СΪ��������
��ͼ����A��B��C��D��E�ڡ�O�ϣ�����ACE=25�㣬��BDE=15�㣬��Բ�Ľǡ�AOB�Ĵ�СΪ��������| A�� | 90�� | B�� | 85�� | C�� | 80�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
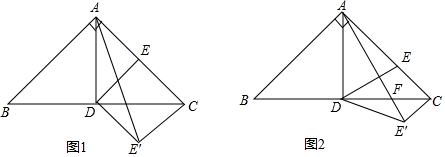
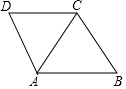 ��ͼ����ABC���ACD��Ϊ�������Σ��ơ�ABC�ı���ij����ת����ABC���ACD�غϣ������ĵ��У�����������
��ͼ����ABC���ACD��Ϊ�������Σ��ơ�ABC�ı���ij����ת����ABC���ACD�غϣ������ĵ��У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��4 | B�� | a��4 | C�� | a��4 | D�� | 1��a��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | .1 �� | B�� | 2 �� | C�� | .3 �� | D�� | .4 �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com