
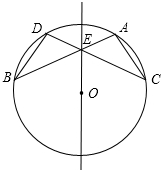
 (2013•金平区模拟)如图,在⊙O中,弦AB与DC相交于点E,DB=AC.
(2013•金平区模拟)如图,在⊙O中,弦AB与DC相交于点E,DB=AC.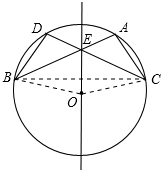 (1)证明:∵在△BDE与△CAE中,
(1)证明:∵在△BDE与△CAE中,
|


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
 (2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是
(2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com