
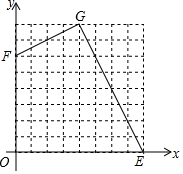
 如图,在平面直角坐标系xOy中,E(8,0),F(0,6).
如图,在平面直角坐标系xOy中,E(8,0),F(0,6).分析 (1)先利用勾股定理分别计算三边长,再利用勾股定理的逆定理可得:∠FGE=90°;
(2)构建全等三角形:△APF≌△MEP,构建P的位置,根据三角形全等得到正方形.
解答  解:(1)如图1,连接EF,
解:(1)如图1,连接EF,
由勾股定理得:FG2=22+42=20,
GE2=42+82=80,
EF2=62+82=100,
∴FG2+GE2=EF2,
∴∠FGE=90°,
故答案为:90°;
(2)如图2,过P作PM⊥x轴于M,当P(7,7),PM为分割线;
根据格点的长度易得:△APF≌△MEP≌△BFP,
∴∠APF=∠MEP,
∵∠MEP+∠MPE=90°,
∴∠APF+∠MPE=90°,
即∠FPE=90°,
四边形OEPF将△EPM剪下放在△BFP上,构建正方形BOMP;
故答案为:(7,7).
点评 本题考查了三角形全等的性质和判定、勾股定理及其逆定理、正方形的判定,熟练掌握勾股定理及其逆定理是关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )
如图,由4个小正方形组成的方格中,△ABC的顶点都在格点上,在这个方格中再画出一个三角形,使它的顶点都在格点上,且与△ABC关于某条直线成轴对称,这样的三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+1>b+1 | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 4-3a>4-3b | D. | 3a-4>3b-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<-1 | B. | 1<k<2 | C. | k<1 | D. | -1<k<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com