
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
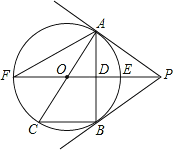
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
【答案】(1)证明见解析(2)EF2=4ODOP,证明见解析(3)![]() ,
,![]()
【解析】解:(1)连接OB,

∵PB是⊙O的切线,∴∠PBO=90°。
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB。
又∵PO=PO,∴△PAO≌△PBO(SAS)。
∴∠PAO=∠PBO=90°。∴直线PA为⊙O的切线。
(2)EF2=4ODOP。证明如下:
∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°。
∴∠OAD=∠OPA。∴△OAD∽△OPA,∴![]() ,即OA2=ODOP。
,即OA2=ODOP。
又∵EF=2OA,∴EF2=4ODOP。
(3)∵OA=OC,AD=BD,BC=6,∴OD=![]() BC=3(三角形中位线定理)。
BC=3(三角形中位线定理)。
设AD=x,
∵tan∠F=![]() ,∴FD=2x,OA=OF=2x﹣3。
,∴FD=2x,OA=OF=2x﹣3。
在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32,
解得,x1=4,x2=0(不合题意,舍去)。∴AD=4,OA=2x﹣3=5。
∵AC是⊙O直径,∴∠ABC=90°。
又∵AC=2OA=10,BC=6,∴cos∠ACB=![]() 。
。
∵OA2=ODOP,∴3(PE+5)=25。∴PE=![]() 。
。
(1)连接OB,根据垂径定理的知识,得出OA=OB,∠POA=∠POB,从而证明△PAO≌△PBO,然后利用全等三角形的性质结合切线的判定定理即可得出结论。
(2)先证明△OAD∽△OPA,由相似三角形的性质得出OA与OD、OP的关系,然后将EF=2OA代入关系式即可。
(3)根据题意可确定OD是△ABC的中位线,设AD=x,然后利用三角函数的知识表示出FD、OA,在Rt△AOD中,由勾股定理解出x的值,从而能求出cos∠ACB,再由(2)可得OA2=ODOP,代入数据即可得出PE的长。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)的图象如图,有下列 5 个结论:①4a+2b+c>0;②abc<0;③b<a+c;④3b>2c;⑤a+b<m(am+b),(m≠1 的实数);其中正确结论的个数为( )
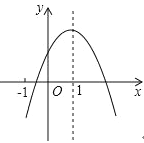
A. 2 个 B. 3 个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( )
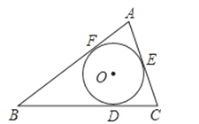
A. AF=4,BD=9,CE=5 B. AF=4,BD=5,CE=9
C. AF=5,BD=4,CE=9 D. AF=9,BD=4,CE=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作平行四边形ABCD的边AB的中点”的尺规作图过程.
已知:平行四边形ABCD.
求作:点M,使点M 为边AB 的中点.
作法:如图,
①作射线DA;
②以点A 为圆心,BC长为半径画弧,
交DA的延长线于点E;
③连接EC 交AB于点M .
所以点M 就是所求作的点.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,EB.
∵四边形ABCD 是平行四边形,
∴AE∥BC.
∵AE= ,
∴四边形EBCA 是平行四边形( )(填推理的依据) .
∴AM =MB ( )(填推理的依据) .
∴点M 为所求作的边AB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
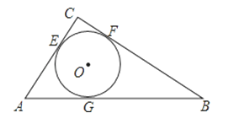
【题目】在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
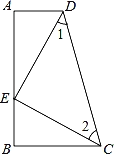
求证:△CED是等腰直角三角形
证明:∵∠1=∠2( )
∴EC= (在一个三角形中,等角对等边)
∵∠A=∠B=90°,AE=BC
∴△AED≌△BCE( )
∴∠AED=∠ ( )
∵∠BCE+∠BEC=90°
∠ +∠BEC=90°(等量代换)
∴∠DEC=90°.
∴△CED是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
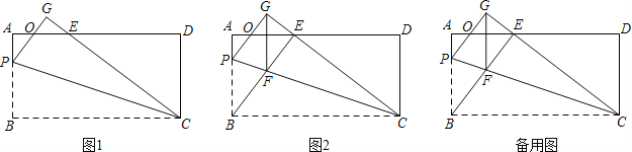
【题目】在矩形ABCD中,AB=12,BC=25,P是线段AB上一点(点P不与A,B重合),将△PBC沿直线PC折叠,顶点B的对应点是点G,CG,PG分别交线段AD于E,O.
(1)如图1,若OP=OE,求证:AE=PB;
(2)如图2,连接BE交PC于点F,若BE⊥CG.
①求证:四边形BFGP是菱形;
②当AE=9,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com