四边形四条边长分别为a，b，c，d，它们满足等式a4+b4+c4+d4=4abcd，试判断四边形的形状．
解：由已知可得
a
4+b
4+c
4+d
4-4abcd=0，
所以（a
4-2a
2b
2+b
4）+（c
4-2c
2d
2+d
4）+（2a
2b
2-4abcd+2c
2d
2）=0，
即（a
2-b
2）
2+（c
2-d
2）
2+2（ab-cd）
2=0．
因为a，b，c，d都是实数，
所以（a
2-b
2）
2≥0，（c
2-d
2）
2≥0，（ab-cd）
2≥0，
所
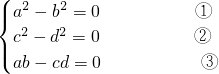
由于a，b，c，d都为正数，所以，解①，②，③有
a=b=c=d．
故此四边形为菱形．
分析：观察a
4+b
4+c
4+d
4=4abcd，运用完全平方式转化为（a
2-b
2）
2+（c
2-d
2）
2+2（ab-cd）
2=0．运用非负数的性质，偶次方大于等于0．因此可解得a、b、c、d间的数值关系．因此可知四边形的形状．
点评：本题考查因式分解的应用、非负数的性质、菱形的判定．解决本题的关键是将等式转化为多项平方和的形式，令其每项均大于等于0，解出a、b、c、d数值关系．
