解不等式组$\left\{\begin{array}{l}{2(x+2)＞3x}\\{\frac{3x-1}{2}≥-2}\end{array}\right.$并将它的解集在数轴上表示出来．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

2．解不等式组$\left\{\begin{array}{l}{2（x+2）＞3x}\\{\frac{3x-1}{2}≥-2}\end{array}\right.$并将它的解集在数轴上表示出来．

分析分别求出每个不等式的解集，在根据“大小小大中间找”即可得答案．

解答解：解不等式2（x+2）＞3x，得：x＜4，
解不等式$\frac{3x-1}{2}$≥-2，得：x≥-1，
∴不等式组的解集为-1≤x＜4，
将解集表示在数轴上如下：

点评本题主要考查解一元一次不等式组的能力，熟练掌握解一元一次不等式组的基本步骤是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

12．解不等式组$\left\{\begin{array}{l}{2（x-1）≤3x+1}\\{\frac{3}{x}＜\frac{x+1}{4}}\end{array}\right.$，并把它的解集在数轴上表示出来．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．

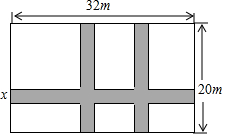如图，在长为32m，宽为20m的矩形空地内，修三条同样宽的道路（阴影部分的矩形为空地内的道路），所修的道路将这块空地分成六块，如果在空地上道路以外的部分种上花草，并且保证种花草的面积是570m²，问道路应多宽？设道路的宽为xm，则下面所列方程正确的是（　　）

	A．	（32-x）（20-x）=32×20-570		B．	32x+2×20x=32×20-570
	C．	（32-2x）（20-x）=570		D．	32x+2×20x-2x²=570

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．在-1，0，1，2，3这五个数中任取两数m，n，则二次函数y=-（x+m）²-n的顶点在x轴上的概率为（　　）

A．

$\frac{1}{5}$

B．

$\frac{1}{4}$

C．

$\frac{2}{5}$

D．

$\frac{1}{2}$

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

17．在平面直角坐标系中，反比例函数y=$\frac{k}{x}$的图象位于第二、四象限，经过点（1，k²-2），则k的值为-1．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．先化简，再代入求值：
（2a+3b）²-（2a+b）（2a-b）-5b（2b+a），其中a=$\frac{1}{3}$，b=-$\frac{1}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．如图，在△ABC中，DE∥BC分别交AB于D，交AC于E，已知CD⊥BE，CD=3、BE=5，求BC+DE的值．小明发现：过点E作EF∥DC，交BC延长线于点F，构造△BEF，经过推理和计算可以解决．
如图①
（1）BC+DE=$\sqrt{34}$；
（2）利用小明的方法写出推理过程
（3）参考小明的方法解决下列问题
如图②，已知?ABCD和矩形ABEF，AC与DF交于点G，FD=FB，且∠BFD=30°，∠EBF=60°，判断AC与DF的数量关系并证明．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．小明想用最大刻度为100℃的温度计测量食用油的沸点温度（远高于100℃），显然不能直接测量，于是他想到了另一种方法．把常温10℃的食用油放在锅内用煤气灶均匀地加热，开始加热后，每隔10s测量一次油温，共测量了4次，测得的数据如下：

时间t/s	0	10	20	30
油温w/℃	10	25	40	55

他测量出把油烧到沸腾所需要的时间是160s，这样就可以确定该食用油的温度．
（1）写出w与r的函数解析式．
（2）求这种食用油沸点的温度．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．计算：
（1）（x-6）（x-3）；
（2）（x+$\frac{1}{2}$）（x-$\frac{1}{3}$）；
（3）（2x+1）（x-3）；
（4）（x-2）（x²+4）．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学