
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BE=CD

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
【答案】(1)△ABC是等腰三角形,理由见解析;(2)点O在∠A的平分线上,理由见解析.
【解析】
试题分析:(1)先利用HL证明Rt△BCD与Rt△CBE全等,然后根据全等三角形对应角相等可得∠ABC=∠ACB,再根据等角对等边的性质可得AB=AC,所以△ABC是等腰三角形;
(2)根据(1)中Rt△BCD≌Rt△CBE,然后利用全等三角形对应边相等可得BD=CE,对应角相等可得∠BCE=∠CBD,然后利用等角对等边可得BO=CO,相减可得OD=OE,再根据到角的两边距离相等的点在角的平分线上即可证明.
解:(1)△ABC是等腰三角形.
理由如下:∵BD、CE是△ABC的高,
∴△BCD与△CBE是直角三角形,
在Rt△BCD与Rt△CBE中,![]() ,
,
∴Rt△BCD≌Rt△CBE(HL),
∴∠ABC=∠ACB,
∴AB=AC,
即△ABC是等腰三角形;
(2)点O在∠A的平分线上.
理由如下:∵Rt△BCD≌Rt△CBE,
∴BD=CE,∠BCE=∠CBD,
∴BO=CO,
∴BD﹣BO=CE﹣CO,
即OD=OE,
∵BD、CE是△ABC的高,
∴点O在∠A的平分线上(到角的两边距离相等的点在角的平分线上).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.

请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学家屠呦呦获得2015年诺贝尔生理学或医学奖,她研发的抗疟新药每年为110万婴幼儿免除了疟疾的危害.其中110万用科学记数法表示为( )
A.11×103
B.1.1×104
C.1.1×106
D.1.1×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?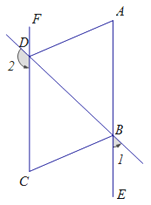
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年5月7日6:30,全球累计新冠肺炎确诊病例超过3 740 000例,3 740 000用科学记数法可表示为( )
A.374×104B.37.4 ×105C.3.74×106D.0.374×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com