
【题目】如图,反比例函数![]() 与一次函数
与一次函数![]() 的图象交于两点A(1,3)、B(n,-1).
的图象交于两点A(1,3)、B(n,-1).
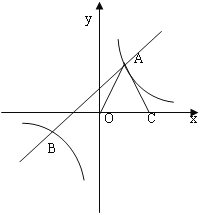
(1)求这两个函数的解析式;
(2)观察图象,请直接写出不等式![]() 的解集;
的解集;
(3)点C为x轴正半轴上一点,连接AO、AC,且AO=AC,求⊿AOC的面积.
【答案】(1)![]() ,y2=x+2;(2)x>1或-3<x<0;(3)3.
,y2=x+2;(2)x>1或-3<x<0;(3)3.
【解析】
试题(1)把点A(1,3)代入反比例函数的解析式,可求出k的值,进而求出其解析式;把点B(n,-1)代入反比例函数的解析式,可求出n的值,即B点坐标;再把A,B两点坐标分别代入一次函数的解析式,便可求出m,b的值,进而求出其解析式.
(2)观察图象即可得解;
(3)由三角形面积计算即可.
试题解析:(1)把A(1,3)的坐标代入![]() ,得m=3,∴反比例函数的解析式为
,得m=3,∴反比例函数的解析式为![]() ,
,
把B(n,-1)的坐标代入![]() ,得-n=3,n=-3.
,得-n=3,n=-3.
把A(1,3)和B(-3,-1)的坐标分别代入![]() ,得
,得![]() ,解得k=1,b=2,
,解得k=1,b=2,
∴一次函数的解析式为y2=x+2;
(2)x>1或-3<x<0;
(3)过A点作AD⊥OC于点D,
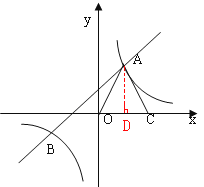
∵AO=AC,
∴OD=CD,
∵A(1,3)在双曲线![]() 图象上,
图象上,
∴OD·AD=3,
∴![]() OC·AD=3,
OC·AD=3,
∴S⊿AOC=3.


科目:初中数学 来源: 题型:
【题目】如图,△ABD内接于⊙O,AB为⊙O的直径,C为弧AD的中点,CH⊥AB于点E,交AD于点P,交⊙O于点H,连接DH,连接BC交AD于点F.下列结论中:①DH⊥CB;②CP=PF;③CH=AD;④APAD=CFCB;⑤若⊙O的半径为5,AF=![]() ,则CH=
,则CH=![]() .正确的有( )
.正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
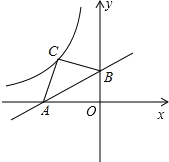
【题目】直线y=![]() x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=
x+3与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,反比例函数y=![]() (x<0)的图象过点C,则m=_____.
(x<0)的图象过点C,则m=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
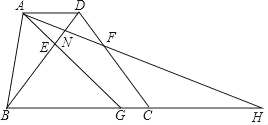
【题目】如图,在梯形ABCD中,AD∥BC,BC=18,DB=DC=15,点E、F分别在线段BD、CD上,DE=DF=5.AE的延长线交边BC于点G,AF交BD于点N、其延长线交BC的延长线于点H.
(1)求证:BG=CH;
(2)设AD=x,△ADN的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)联结FG,当△HFG与△ADN相似时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),顶点为G.
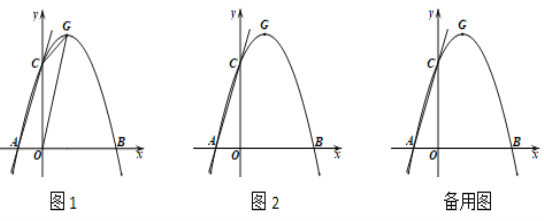
(1)求抛物线和直线AC的解析式;
(2)如图1,设E(m,0)为x正半轴上的一个动点,若△CGE和△CGO的面积满足S△CGE=![]() S△CGO,求点E的坐标;
S△CGO,求点E的坐标;
(3)如图2,设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为ts,点M为射线AC上一动点,过点M作MN∥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程2x2-2x+m+1=0的两个实根.
(1)求实数m的取值范围;
(2)如果m满足不等式7+4x1x2>x12+x22,且m为整数.求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com