
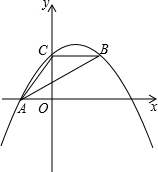
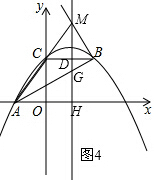
 如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.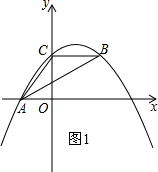 解:(1)如图1,
解:(1)如图1,
|
|
| 1 |
| 6 |
| 5 |
| 6 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| 5 |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 6 |
| t |
| 3 |
| 5 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
| 8 |
| 3 |
| 1 |
| 6 |
| 8 |
| 3 |
| 8 |
| 3 |
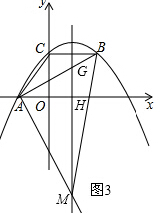
| b |
| 2a |
| ||
2×(-
|
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 11 |
| 4 |
| 11 |
| 4 |
| GH |
| AH |
| AH |
| MH |
| ||
|
| ||
| MH |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 11 |
| 4 |
| 5 |
| 4 |
| BD2+DG2 |
(
|
5
| ||
| 4 |
11
| ||
| 4 |
| AG |
| MG |
| GH |
| GB |
| ||||
| MG |
| ||||
|
| 25 |
| 4 |
| 25 |
| 4 |
| 11 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、6厘米 | B、12厘米 |
| C、24厘米 | D、36厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
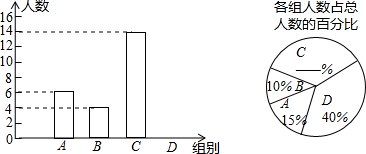
 学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:| 等级 | 成绩(S) | 频数 |
| A | 90<S≤100 | x |
| B | 80<S≤90 | 15 |
| C | 70<S≤80 | 10 |
| D | S≤70 | 3 |
| 合计 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
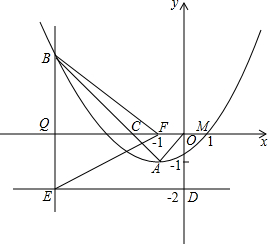 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com